| 2022年高考数学新高考Ⅰ-16(5分)已知椭圆$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a > b > 0)$,$C$的上顶点为$A$,两个焦点为$F_{1}$,$F_{2}$,离心率为$\dfrac{1}{2}$.过$F_{1}$且垂直于$AF_{2}$的直线与$C$交于$D$,$E$两点,$\vert DE\vert =6$,则$\Delta ADE$的周长是____【答案详解】 |
2022年高考数学新高考Ⅰ-17(10分)记$S_{n}$为数列$\{a_{n}\}$的前$n$项和,已知$a_{1}=1$,$\{\dfrac{{S}_{n}}{{a}_{n}}\}$是公差为$\dfrac{1}{3}$的等差数列.
(1)求$\{a_{n}\}$的通项公式;
(2)证明:$\dfrac{1}{a_1}+\dfrac{1}{a_2}+\ldots +\dfrac{1}{a_n} < 2$.【答案详解】 |
2022年高考数学新高考Ⅰ-18(12分)记$\Delta ABC$的内角$A$,$B$,$C$的对边分别为$a$,$b$,$c$,已知$\dfrac{\cos A}{1+\sin A}=\dfrac{\sin 2B}{1+\cos 2B}$.
(1)若$C=\dfrac{2\pi }{3}$,求$B$;
(2)求$\dfrac{{a^2}+{b^2}}{c^2}$的最小值.【答案详解】 |
2022年高考数学新高考Ⅰ-19(12分)如图,直三棱柱$ABC-A_{1}B_{1}C_{1}$的体积为4,△$A_{1}BC$的面积为$2\sqrt{2}$.
(1)求$A$到平面$A_{1}BC$的距离;
(2)设$D$为$A_{1}C$的中点,$AA_{1}=AB$,平面$A_{1}BC\bot$平面$ABB_{1}A_{1}$,求二面角$A-BD-C$的正弦值.
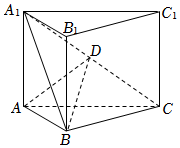 【答案详解】 【答案详解】 |
2022年高考数学新高考Ⅰ-20(12分)一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系,在已患该疾病的病例中随机调查了100例(称为病例组),同时在未患该疾病的人群中随机调查了100人(称为对照组),得到如下数据:
(1)能否有$99%$的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异?
(2)从该地的人群中任选一人,$A$表示事件“选到的人卫生习惯不够良好”, $B$表示事件“选到的人患有该疾病”, $\dfrac{P(B\vert A)}{P(\overline{B}\vert A)}$与$\dfrac{P(B\vert \overline{A})}{P(\overline{B}\vert \overline{A})}$的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为$R$.
(ⅰ)证明:$R=\dfrac{P(A\vert B)}{P(\overline{A}\vert B)}\cdot \dfrac{P(\overline{A}\vert \overline{B})}{P(A\vert \overline{B})}$;
(ⅱ)利用该调查数据,给出$P(A\vert B)$,$P(A\vert \overline{B})$的估计值,并利用(ⅰ)的结果给出$R$的估计值.
附:$K^{2}=\dfrac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| $P(K^{2}\geqslant k)$ | 0.050 | 0.010 | 0.001 | | $k$ | 3.841 | 6.635 | 10.828 |
【答案详解】 |

