|
2022年高考数学新高考Ⅰ-13<-->2022年高考数学新高考Ⅰ-15
(5分)写出与圆$x^{2}+y^{2}=1$和$(x-3)^{2}+(y-4)^{2}=16$都相切的一条直线的方程 $x=-1$(填$3x+4y-5=0$,$7x-24y-25=0$都正确) .
分析:由题意画出图形,可得两圆外切,由图可知,与两圆都相切的直线有三条.分别求出三条切线方程,则答案可求.
解:圆$x^{2}+y^{2}=1$的圆心坐标为$O(0,0)$,半径$r_{1}=1$,
圆$(x-3)^{2}+(y-4)^{2}=16$的圆心坐标为$C(3,4)$,半径$r_{2}=4$,
如图:
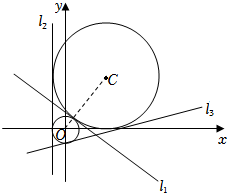
$\because \vert OC\vert =r_{1}+r_{2}$,$\therefore$两圆外切,由图可知,与两圆都相切的直线有三条.
$\because$${k}_{OC}=\dfrac{4}{3}$,$\therefore l_{1}$的斜率为$-\dfrac{3}{4}$,设直线$l_{1}:y=-\dfrac{3}{4}x+b$,即$3x+4y-4b=0$,
由$\dfrac{\vert -4b\vert }{5}=1$,解得$b=\dfrac{5}{4}$(负值舍去),则$l_{1}:3x+4y-5=0$;
由图可知,$l_{2}:x=-1$;$l_{2}$与$l_{3}$关于直线$y=\dfrac{4}{3}x$对称,
联立$\left\{\begin{array}{l}{x=-1}\\ {y=\dfrac{4}{3}x}\end{array}\right.$,解得$l_{2}$与$l_{3}$的一个交点为$(-1,-\dfrac{4}{3})$,在$l_{2}$上取一点$(-1,0)$,
该点关于$y=\dfrac{4}{3}x$的对称点为$(x_{0}$,$y_{0})$,则$\left\{\begin{array}{l}{\dfrac{{y}_{0}}{2}=\dfrac{4}{3}\cdot \dfrac{{x}_{0}-1}{2}}\\ {\dfrac{{y}_{0}}{{x}_{0}+1}=-\dfrac{3}{4}}\end{array}\right.$,解得对称点为$(\dfrac{7}{25}$,$-\dfrac{24}{25})$.
$\therefore$${k}_{{l}_{3}}=\dfrac{-\dfrac{24}{25}+\dfrac{4}{3}}{\dfrac{7}{25}+1}=\dfrac{7}{24}$,则$l_{3}:y=\dfrac{7}{24}(x+1)-\dfrac{4}{3}$,即$7x-24y-25=0$.
$\therefore$与圆$x^{2}+y^{2}=1$和$(x-3)^{2}+(y-4)^{2}=16$都相切的一条直线的方程为:
$x=-1$(填$3x+4y-5=0$,$7x-24y-25=0$都正确).
故答案为:$x=-1$(填$3x+4y-5=0$,$7x-24y-25=0$都正确).
点评:本题考查圆的切线方程的求法,考查圆与圆位置关系的应用,考查运算求解能力,是中档题.
2022年高考数学新高考Ⅰ-13<-->2022年高考数学新高考Ⅰ-15
全网搜索"2022年高考数学新高考Ⅰ-14"相关
|

