2024年高考数学天津16(14分)在$\Delta ABC$中$,\cos B=\dfrac{9}{16}$,$b=5$,$\dfrac{a}{c}=\dfrac{2}{3}$.
(1)求$a$;
(2)求$\sin A$;
(3)求$\cos (B-2A)$.【答案详解】 |
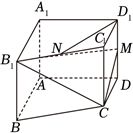
2024年高考数学天津17(15分)已知四棱锥$ABCD-A_{1}B_{1}C_{1}D_{1}$中,底面$ABCD$为梯形,$AB//CD$,$A_{1}A\bot$平面$ABCD$,$AD\bot AB$,其中$AB=AA_{1}=2$,$AD=DC=1$.$N$是$B_{1}C_{1}$的中点,$M$是$DD_{1}$的中点.
(1)求证:$D_{1}N//$平面$CB_{1}M$;
(2)求平面$CB_{1}M$与平面$BB_{1}CC_{1}$的夹角余弦值;
(3)求点$B$到平面$CB_{1}M$的距离.
 【答案详解】 【答案详解】 |
2024年高考数学天津18(15分)已知椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a > b > 0)$的离心率$e=\dfrac{1}{2}$,左顶点为$A$,下顶点为$B$,$C$是线段$OB$的中点,其中$S_{\Delta ABC}=\dfrac{3\sqrt{3}}{2}$.
(1)求椭圆方程.
(2)过点$(0,-\dfrac{3}{2})$的动直线与椭圆有两个交点$P$,$Q$,在$y$轴上是否存在点$T$使得$\overrightarrow{TP}\cdot \overrightarrow{TQ}\leqslant 0$恒成立.若存在,求出这个$T$点纵坐标的取值范围;若不存在,请说明理由.【答案详解】 |
2024年高考数学天津1915分)已知数列$\{a_{n}\}$是公比大于0的等比数列,其前$n$项和为$S_{n}$,若$a_{1}=1$,$S_{2}=a_{3}-1$.
(1)求数列$\{a_{n}\}$前$n$项和$S_{n}$;
(2)设$b_{n}=\left\{\begin{array}{l}{k,n={a}_{k}}\\ {{b}_{n-1}+2k,{a}_{k} < n < {a}_{k+1}}\end{array}\right.$,$b_{1}=1$,其中$k$是大于1的正整数.
$(i)$当$n=a_{k+1}$时,求证:$b_{n-1}\geqslant a_{k}\cdot b_{n}$;
$(ii)$求$\sum\limits_{i=1}^{{S}_{n}}{b}_{i}$.【答案详解】 |
2024年高考数学天津20(16分)设函数$f(x)=x\ln x$.
(1)求$f(x)$图像上点$(1$,$f$(1)$)$处的切线方程;
(2)若$f(x)\geqslant a(x-\sqrt{x})$在$x\in (0,+\infty )$时恒成立,求$a$的值;
(3)若$x_{1}$,$x_{2}\in (0,1)$,证明$\vert f(x_1)-f(x_2)\vert \leqslant \vert x_1-x_2\vert ^\dfrac{1}{2}$.【答案详解】 |

