|
2024年高考数学天津8<-->2024年高考数学天津10
(5分)一个五面体$ABC-DEF$.已知$AD//BE//CF$,且两两之间距离为1.并已知$AD=1$,$BE=2$,$CF=3$.则该五面体的体积为( )
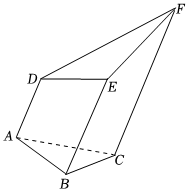
A.$\dfrac{\sqrt{3}}{6}$ B.$\dfrac{3\sqrt{3}}{4}+\dfrac{1}{2}$ C.$\dfrac{\sqrt{3}}{2}$ D.$\dfrac{3\sqrt{3}}{4}-\dfrac{1}{2}$
答案:$C$
分析:根据题意,分别延长$AD$、$BE$到$G$、$H$,使$AG$、$BH$、$CF$平行且相等,得到三棱柱$ABC-GHF$,根据四边形$ABED$与四边形$HGDE$全等,利用锥体的体积公式得到$V_{F-ABED}=V_{F-HGDE}=\dfrac{1}{3}V_{ABC-GHF}$,然后求出$ABC-GHF$的体积,进而算出该五面体的体积,可得答案.
解:延长$AD$到$G$,使$DG=2$,延长$BE$到$H$,使$EH=1$,连接$AF$、$BF$,
可得$AG=BH=CF=3$,结合$AG//BH//CF$,可知$ABC-GHF$为三棱柱,
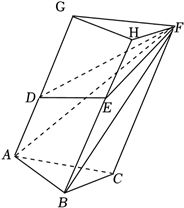
因为四边形$ABED$与四边形$HGDE$全等,所以$V_{F-ABED}=V_{F-HGDE}=\dfrac{1}{3}V_{ABC-GHF}$,
由$AG//BH//CF$,且它们两两之间的距离为1.可知:
当$ABC-GHF$为正三棱柱时,底面边长为1,高为3,此时$V_{ABC-GHF}=\dfrac{\sqrt{3}}{4}\times 1^{2}\times 3=\dfrac{3\sqrt{3}}{4}$.
根据棱柱的性质,若$ABC-GHF$为斜三棱柱,体积也是$\dfrac{3\sqrt{3}}{4}$,
因此,$V_{F-HGDE}=\dfrac{1}{3}V_{ABC-GHF}=\dfrac{\sqrt{3}}{4}$,可得该五面体的体积$V=V_{ABC-GHF}-V_{F-HGDE}=\dfrac{\sqrt{3}}{2}$.
故选:$C$.
点评:本题主要考查棱柱的定义与性质、柱体与锥体的体积公式及其应用等知识,考查了计算能力、图形的理解能力,属于中档题.
2024年高考数学天津8<-->2024年高考数学天津10
全网搜索"2024年高考数学天津9"相关
|

