解答题
全国卷Ⅰ(理)
2004年
19.(本小题满分12分)
已知![]() 求函数
求函数![]() 的单调区间.
的单调区间.
2005年
(19)(本大题满分12分)
设等比数列![]() 的公比为
的公比为![]() ,前n项和
,前n项和![]()
![]()
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)设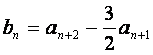 ,记
,记![]() 的前n项和为
的前n项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小
的大小![]()
2006年
(19)(本小题满分12分)
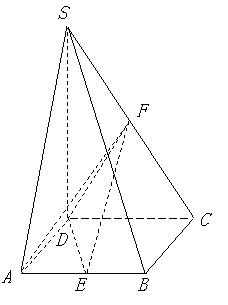
如图,l1、l2是互相垂直的异面直线,MN是它们的公垂线段,点A、B在l1上,C在
l2上,AM=MB=MN。
(Ⅰ)证明![]() ;
;
(Ⅱ)若![]() ,求NB与平面ABC所成角的余弦值。
,求NB与平面ABC所成角的余弦值。
2007年
(19)(本小题满分12分)
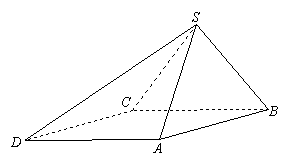 四棱锥
四棱锥![]() 中,底面
中,底面![]() 为平行四边形,侧面
为平行四边形,侧面![]() 底面
底面![]() .已知
.已知![]() ,
,
![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
全国卷Ⅱ(理)
2004年
19.(本小题满分12分)
数列![]() 的前n项和记为Sn,已知
的前n项和记为Sn,已知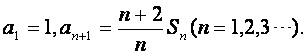 证明:
证明:
(Ⅰ)数列![]() 是等比数列;
是等比数列;
(Ⅱ)![]()
2005年
(19)(本小题满分12分)
甲、乙两队进行一场排球比赛.根据以往经验,单局比赛甲队胜乙队的概率为0.6,
本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没
有影响.令![]() 为本场比赛的局数.求
为本场比赛的局数.求![]() 的概率分布和数学期望.(精确到0.0001)
的概率分布和数学期望.(精确到0.0001)
2006年
(19)(本小题满分12分)
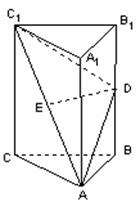
如图,在直三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点。
的中点。
(I)证明:ED为异面直线![]() 与
与![]() 的公垂线;
的公垂线;
(II)设![]() 求二面角
求二面角![]() 的大小。
的大小。
2007年
19.(本小题满分12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,
侧棱![]() 底面
底面![]() 分别为
分别为![]() 的中点.
的中点.
(1)证明![]() 平面
平面![]() ;
;
(2)设![]() ,求二面角
,求二面角![]() 的大小.
的大小.
全国卷Ⅲ(理)
2004年
19.(本小题满分12分)某村计划建造一个室内面积为800![]() 的矩形蔬菜温室。
的矩形蔬菜温室。
在温室内,沿左.右两侧与后侧内墙各保留1![]() 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3![]() 宽
宽
的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
2005年
19.(本小题满分12分)
![]() 中,内角
中,内角![]() .
.![]() .
.![]() 的对边分别为
的对边分别为![]() .
.![]() .
.![]() ,已知
,已知![]() .
.![]() .
.![]() 成等比数列,且
成等比数列,且![]()
![]()
![]()
(1)求![]() 的值;
的值;
(2)若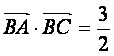 ,求
,求![]() 的值
的值![]()
全国卷Ⅳ(理)
2004年
19.(本小题满分12分)
某同学参加科普知识竞赛,需回答三个问题.竞赛规则规定:
每题回答正确得100分,回答不正确得-100分.假设这名同学每题回答
正确的概率均为0.8,且各题回答正确与否相互之间没有影响.
(Ⅰ)求这名同学回答这三个问题的总得分![]() 的概率分布和数学期望;
的概率分布和数学期望;
(Ⅱ)求这名同学总得分不为负分(即![]() ≥0)的概率.
≥0)的概率.
2007年
北京卷(理)
2004年
(17)(本小题满分14分)
如图,过抛物线![]() 上一定点P(
上一定点P(![]() )(
)(![]() ),作两条直线
),作两条直线
分别交抛物线于A(![]() ),B(
),B(![]() )
)
(I)求该抛物线上纵坐标为![]() 的点到其焦点F的距离
的点到其焦点F的距离
(II)当PA与PB的斜率存在且倾斜角互补时,求![]() 的值,并证明直线AB
的值,并证明直线AB
的斜率是非零常数
2005年
17 (本小题共13分)
甲、乙俩人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]()
![]()
(Ⅰ)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望
的概率分布及数学期望![]() ;
;
(Ⅱ)求乙至多击中目标2次的概率;
(Ⅲ)求甲恰好比乙多击中目标2次的概率![]()
2006年
(17)(本小题共14分)
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,
且PA=AB,点E是PD的中点.
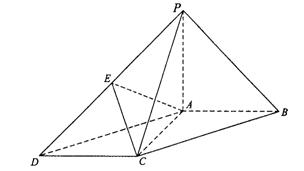
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PB∥平面AEC;
(Ⅲ)求二面角E-AC-B的大小.
2007年
17.(本小题共14分)
矩形![]() 的两条对角线相交于点
的两条对角线相交于点![]() ,
,![]() 边所在直线的方程为
边所在直线的方程为![]() ,
,
点![]() 在
在![]() 边所在直线上.
边所在直线上.
(I)求![]() 边所在直线的方程;
边所在直线的方程;
(II)求矩形![]() 外接圆的方程;
外接圆的方程;
(III)若动圆![]() 过点
过点![]() ,且与矩形
,且与矩形![]() 的外接圆外切,求动圆
的外接圆外切,求动圆![]() 的圆心的轨迹方程.
的圆心的轨迹方程.
天津卷(理)
2004年
19. (本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,
PD=DC,E是PC的中点,作EF⊥PB交PB于点F。
(1)证明PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C—PB—D的大小。
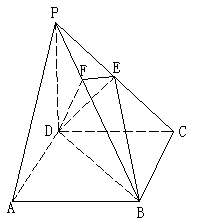
2005年
(19)(本小题满分12分)
如图,在斜三棱柱![]() 中,
中,![]() ,
,
侧面![]() 与底面ABC所成的二面角为
与底面ABC所成的二面角为![]() ,E、F分别是棱
,E、F分别是棱![]() 的中点
的中点
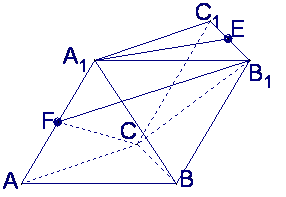 (Ⅰ)求
(Ⅰ)求![]() 与底面ABC所成的角
与底面ABC所成的角
(Ⅱ)证明![]() ∥平面
∥平面![]()
(Ⅲ)求经过![]() 四点的球的体积
四点的球的体积
2006年
(19)(本小题满分12分)
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,
面CDE是等边三角形,棱EF![]()
![]() BC.
BC.
(Ⅰ)证明FO∥平面CDE;
(Ⅱ)设BC=![]() CD,证明EO⊥平面CDF.
CD,证明EO⊥平面CDF.
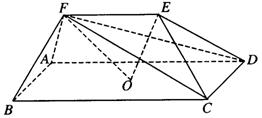
2007年
19.(本小题满分12分)
如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,
![]() ,
,![]() 是
是![]() 的中点.
的中点.
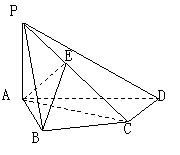 (Ⅰ)证明
(Ⅰ)证明![]() ;
;
(Ⅱ)证明![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
上海卷(理)
2004年
19、(本题满分14分) 第1小题满分6分, 第2小题满分8分
记函数f(x)=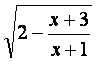 的定义域为A,
g(x)=lg[(x-a-1)(2a-x)](a<1)
的定义域为A,
g(x)=lg[(x-a-1)(2a-x)](a<1)
的定义域为B.
(1) 求A;
(2)
若B![]() A,
求实数a的取值范围.
A,
求实数a的取值范围.
2005年
19.点A、B分别是椭圆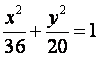 长轴的左、右焦点,点F是椭圆的右焦点
长轴的左、右焦点,点F是椭圆的右焦点![]() 点P在椭圆上,
点P在椭圆上,
且位于x轴上方,![]()
![]()
(1)求P点的坐标;
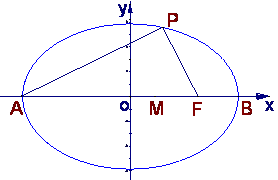 (2)设M是椭圆长轴AB上的一点,M到直线AP的
(2)设M是椭圆长轴AB上的一点,M到直线AP的
距离等于![]() ,求椭圆上的点到点M的距离d的最小值
,求椭圆上的点到点M的距离d的最小值![]()
2006年
19.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分)
在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60![]() ,对角线AC与BD
,对角线AC与BD
相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60![]() .
.
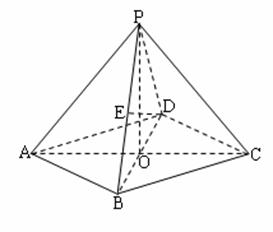
(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的大小(结果用反三角函数值表示).
2007年
18.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
近年来,太阳能技术运用的步伐日益加快.2002年全球太阳电池的年生产量
达到670兆瓦,年生产量的增长率为34%.以后四年中,年生产量的增长率逐年递
增2%(如,2003年的年生产量的增长率为36%).
(1)求2006年全球太阳电池的年生产量(结果精确到0.1兆瓦);
(2)目前太阳电池产业存在的主要问题是市场安装量远小于生产量,2006年
的实际安装量为1420兆瓦.假设以后若干年内太阳电池的年生产量的增长率保持
在42%,到2010年,要使年安装量与年生产量基本持平(即年安装量不少于年生产
量的95%),这四年中太阳电池的年安装量的平均增长率至少应达到多少(结果精
确到0.1%)?
辽宁卷(理)
2004年
19.(本小题满分12分)
设椭圆方程为 ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,
点P满足![]() ,点N的坐标为
,点N的坐标为![]() ,当l绕点M旋转时,求:
,当l绕点M旋转时,求:
(1)动点P的轨迹方程;
(2)![]() 的最小值与最大值.
的最小值与最大值.
2005年
19.(本小题满分12分)
已知函数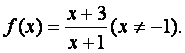 设数列
设数列![]() }满足
}满足![]() ,数列
,数列![]() }满足
}满足
![]()
(Ⅰ)用数学归纳法证明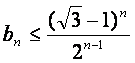 ;
;
(Ⅱ)证明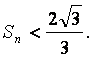
2006年(理)
(19) (本小题满分12分)
现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、
1.17万元的概率分别为![]() 、
、![]() 、
、![]() ;已知乙项目的利润与产品价格的调整有关,在每
;已知乙项目的利润与产品价格的调整有关,在每
次调整中,价格下降的概率都是![]() ,设乙项目产品价格在一年内进行2次独立
,设乙项目产品价格在一年内进行2次独立
的调整,记乙项目产品价格在一年内的下降次数为![]() ,对乙项目每投资十万元,
,对乙项目每投资十万元,
![]() 取
取
0、1、2时,
一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量![]() 、
、![]() 分别
分别
表示对甲、乙两项目各投资十万元一年后的利润.
(I)
求![]() 、
、![]() 的概率分布和数学期望
的概率分布和数学期望![]() 、
、![]() ;
;
(II)
当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
2007年
19.(本小题满分12分)
某企业准备投产一批特殊型号的产品,已知该种产品的成本![]() 与产量
与产量![]() 的函数关系式为
的函数关系式为
 该种产品的市场前景无法确定,有三种可能出现的情况,
该种产品的市场前景无法确定,有三种可能出现的情况,
各种情形发生的概率及产品价格![]() 与产量
与产量![]() 的函数关系式如下表所示:
的函数关系式如下表所示:
|
市场情形 |
概率 |
价格 |
|
好 |
0.4 |
|
|
中 |
0.4 |
|
|
差 |
0.2 |
|
设![]() 分别表示市场情形好、中差时的利润,随机变量
分别表示市场情形好、中差时的利润,随机变量![]() ,表示当产量为
,表示当产量为![]() ,
,
而市场前景无法确定的利润.
(I)分别求利润![]() 与产量
与产量![]() 的函数关系式;
的函数关系式;
(II)当产量![]() 确定时,求期望
确定时,求期望![]() ;
;
(III)试问产量![]() 取何值时,
取何值时,![]() 取得最大值.
取得最大值.
江苏卷
2004年
19.制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.
某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大
盈利率分别为100﹪和50﹪,可能的最大亏损分别为30﹪和10﹪. 投资人计
划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投
资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
2005年
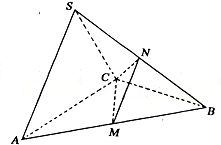
21.(本小题满分14分,第一小问满分6分,第二.第三小问满分各4分)
 如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,
如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,![]() ,
,
![]()
![]()
⑴求异面直线CD与SB所成的角(用反三角函数值表示);
⑵证明:BC⊥平面SAB;
⑶用反三角函数值表示二面角B—SC—D的大小![]() (本小问不必写出解答过程)
(本小问不必写出解答过程)
2006年
(19)(本小题满分14分,第一小问满分4分,第二小问满分5分,
第三小问满分5分)
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足
AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到![]() 的位置,
的位置,
使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示)

2007年
19.(本题满分14分)
如图,在平面直角坐标系![]() 中,过
中,过![]() 轴正方向上一点
轴正方向上一点![]() 任作一直线,
任作一直线,
与抛物线![]() 相交于
相交于![]() 两点.一条垂直于
两点.一条垂直于![]() 轴的直线,分别与线段
轴的直线,分别与线段![]() 和
和
直线![]() 交于点
交于点![]() .
.
(1)若![]() ,求
,求![]() 的值;(5分)
的值;(5分)
(2)若![]() 为线段
为线段![]() 的中点,
的中点,
求证:![]() 为此抛物线的切线;(5分)
为此抛物线的切线;(5分)
(3)试问(2)的逆命题是否成立?说明理由.(4分)
浙江卷(理)
2004年
(19)(本题满分12分)
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
 AB=
AB=![]() ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。
(Ⅰ)求证AM∥平面BDE;
(Ⅱ)求二面角A—DF—B的大小;
2005年
17.如图,已知椭圆的中心在坐标原点,焦点![]() 在x轴上,长轴
在x轴上,长轴![]() 的长为4,
的长为4,
左准线![]() 与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
 (Ⅰ)求椭圆的方程;
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线![]() :x=m(|m|>1),P为
:x=m(|m|>1),P为![]() 上的动点,
上的动点,
使![]() 最大的点P记为Q,求点Q的坐标(用m表示).
最大的点P记为Q,求点Q的坐标(用m表示).
2006年
(17)如图,在四棱锥P-ABCD中,底面为直角梯形,AD//BC,![]() BAD=
BAD=![]() ,
,
PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.

(Ⅰ)求证:PB⊥DM;
(Ⅱ) 求CD与平面ADMN所成的角。
2007年
(20)(本题14分)如图,直线![]() 与椭圆
与椭圆
交于![]() 两点,
两点,
记![]() 的面积为
的面积为![]() .
.
(I)求在![]() ,
,![]() 的条件下,
的条件下,![]() 的最大值;
的最大值;
 (II)当
(II)当![]() ,
,![]() 时,求直线
时,求直线![]() 的方程.
的方程.
福建卷(理)
2004年
(19)(本小题满分12分)
 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,
SA=SC=2![]() ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角N-CM-B的大小;
(Ⅲ)求点B到平面CMN的距离。
2005年
19.(本小题满分12分)
已知函数 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
2006年
(19)(本小题满分12分)
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量![]() (升)关于行驶
(升)关于行驶
速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为:
 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
2007年
19.(本小题满分12分)
某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司
交![]() 元(
元(![]() )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为![]() 元(
元(![]() )时,
)时,
一年的销售量为![]() 万件.
万件.
(Ⅰ)求分公司一年的利润![]() (万元)与每件产品的售价
(万元)与每件产品的售价![]() 的函数关系式;
的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,分公司一年的利润![]() 最大,
最大,
并求出![]() 的最大值
的最大值![]() .
.
湖北卷(理)
2004年
(19)(本小题满分12分)
 如图,在Rt△ABC中,已知BC=a,若长为2
a的线段P Q以点A为中点,
如图,在Rt△ABC中,已知BC=a,若长为2
a的线段P Q以点A为中点,
问![]() 与
与![]() 的夹角θ取何值时
的夹角θ取何值时![]() ,
,![]() 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。
2005年
19.(本小题满分12分)
某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有4次参加
考试的机会,一量某次考试通过,便可领取驾照,不再参加以后的考试,否则
就一直考到第4次为止![]() 如果李明决定参加驾照考试,设他每次参加考试通过的
如果李明决定参加驾照考试,设他每次参加考试通过的
概率依次为0.6,0.7,0.8,0.9![]() 求在一年内李明参加驾照考试次数
求在一年内李明参加驾照考试次数![]() 的分布列
的分布列
和![]() 的期望,并求李明在一所内领到驾照的概率
的期望,并求李明在一所内领到驾照的概率
2006年
18.(本小题满分12分)
如图,在棱长为1的正方体ABCD—A1B1C1D1中,P是侧棱CC1上的一点,CP=m。

(Ⅰ)试确定m,使得直线AP与平面BDD1B1所成角的正切值为![]() ;
;
(Ⅱ)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影
垂直于AP,并证明你的结论。
2007年
18.(本小题满分12分)
如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,
![]()
 .
.
(I)求证:平面![]()
![]() ;
;
(II)当解![]() 变化时,求直线
变化时,求直线![]() 与平面
与平面![]() 所成的角的取值范围.
所成的角的取值范围.
湖南卷(理)
2004年
(19) (本小题满分12分)
如图,在底面是菱形的四棱锥P—ABCD中,![]()
点E在PD上,且PE:ED= 2: 1.
(Ⅰ)证明 PA⊥平面ABCD;
 (Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小:
(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小:
(Ⅲ)在棱PC上是否存在一点F, 使BF∥平面AEC?证明你的结论.
2005年
18.(本小题满分14分)
某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别
是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开
该城市时游览的景点数与没有游览的景点数之差的绝对值.
(Ⅰ)求ξ的分布及数学期望;
(Ⅱ)记“函数f(x)=x2-3ξx+1在区间[2,+∞![]() 上单调递增”为
上单调递增”为
事件A,求事件A的概率.
2006年
18.(本小题满分14分)
如图4,己知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.

(Ⅰ)证明PQ⊥平面ABCD;
(Ⅱ)求异面直线AQ与PB所成的角;
(Ⅲ)求点P到平面QAD的距离.
2007年
18.(本小题满分12分)
如图2,![]() 分别是矩形
分别是矩形![]() 的边
的边![]() 的中点,
的中点,![]() 是
是![]() 上的一点,将
上的一点,将![]() ,
,
![]() 分别沿
分别沿![]() 翻折成
翻折成![]() ,
,![]() ,并连结
,并连结![]() ,使得平面
,使得平面![]() 平面
平面![]() ,
,
![]() ,且
,且![]() .连结
.连结![]() ,如图3.
,如图3.


图2 图3
(I)证明:平面![]() 平面
平面![]() ;
;
(II)当![]() ,
,![]() ,
,![]() 时,求直线
时,求直线![]() 和平面
和平面![]() 所成的角.
所成的角.
广东卷(理)
2004年
19. (12分)设函数![]()
(1)
证明:
当0< a < b ,且![]() 时,ab
>1;
时,ab
>1;
(2)
点P
(x0, y0 ) (0< x0 <1 )在曲线![]() 上,求曲线在点P处的
上,求曲线在点P处的
切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).
2005年
17.(本小题满分14分)
在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B
满足AO⊥BO(如图4所示).
(Ⅰ)求△AOB的重心G(即三角形三条

中线的交点)的轨迹方程;
(Ⅱ)△AOB的面积是否存在最小值?若存在,
请求出最小值;若不存在,请说明理由.
2006年
17.(本小题满分14分)
如图所示,AF、DE分别是⊙![]() 、⊙
、⊙![]() 1的直径。AD与两圆所在的平面均
1的直径。AD与两圆所在的平面均
垂直,AD=8,BC是⊙![]() 的直径,AB=AC=6,OE//AD。
的直径,AB=AC=6,OE//AD。

(Ⅰ)求二面角B-AD-F的大小;
(Ⅱ)求直线BD与EF所成的角。
2007年
18.(本小题满分14分)
在平面直角坐标系![]() ,已知圆心在第二象限、半径为
,已知圆心在第二象限、半径为![]() 的圆
的圆![]() 与直线
与直线![]() 相切于
相切于
坐标原点![]() .椭圆
.椭圆 与圆
与圆![]() 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)试探究圆![]() 上是否存在异于原点的点
上是否存在异于原点的点![]() ,使
,使![]() 到椭圆右焦点
到椭圆右焦点![]() 的距离等于线
的距离等于线
段![]() 的长,若存在,请求出点
的长,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
重庆卷(理)
2004年
19.(本小题满分12分)
如图,四棱锥P-ABCD的底面是正方形,
![]()
(1) 证明MF是异面直线AB与PC的公垂线;
(2)
若![]() ,求直线AC与平面EAM所成角的正弦值。
,求直线AC与平面EAM所成角的正弦值。

2005年
19.(本小题满分13分)
已知![]() ,讨论函数
,讨论函数![]() 的极值点的个数
的极值点的个数![]()
2006年
(19)(本小题满分13分)
如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() 为直角,
为直角,![]()
![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、CD的中点。
、CD的中点。
(Ⅰ)试证:![]() 平面
平面![]() ;
;
(Ⅱ)设PA=K·AB,且二面角![]() 的平面角大于
的平面角大于![]() ,求
,求![]() 的取值范围。
的取值范围。

2007年
19.(本小题满分13分,其中(Ⅰ)小问8分,(Ⅱ)小问5分)
 如题(19)图,在直三棱柱
如题(19)图,在直三棱柱![]() 中,
中,
![]() ,
,![]() ,
,![]() ;
;
点![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,
,
四棱锥![]() 与直三棱柱的体积之比为
与直三棱柱的体积之比为![]() .
.
(Ⅰ)求异面直线![]() 与
与![]() 的距离;
的距离;
(Ⅱ)若![]() ,求二面角
,求二面角![]() 的平面角的正切值.
的平面角的正切值.
山东卷(理)
2005年
(19) (本小题满分12分)
已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]()
![]() .
.
(Ⅰ)求m与n的关系表达式;
(Ⅱ)求![]() 的单调区间;
的单调区间;
(Ⅲ)当![]() 时,函数
时,函数![]() 的图象上任意一点的切线斜率恒大于3m,
的图象上任意一点的切线斜率恒大于3m,
求m的取值范围![]()
2006年
19.(本小题满分12分)
如图,已知平面A1B1C1平行于三棱锥V-ABC的底面ABC,等边△AB1C
所在的平面与底面ABC垂直,且∠ACB=90°.设AC=2a,BC=a.

(Ⅰ)求证直线B1C1是异面直线AB1与A1C1的公垂线;
(Ⅱ)求点A到平面VBC的距离;
(Ⅲ)求二面角A-VB-C的大小.
2007年
(19)(本小题满分12分)
 如图,在直四棱柱
如图,在直四棱柱![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)设![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
江西卷(理)
2005年
19.(本小题满分12分)
A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面
朝上时A赢得B一张卡片,否则B赢得A一张卡片.规定掷硬币的次数达9次时,或
在此前某人已赢得所有卡片时游戏终止.设![]() 表示游戏终止时掷硬币的次数.
表示游戏终止时掷硬币的次数.
(1)求![]() 的取值范围;
的取值范围;
(2)求![]() 的数学期望E
的数学期望E![]() .
.
2006年
19.(本小题满分12分)
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的
点,线段MN经过△ABC的中心G.设∠MGA=α(![]() ≤α≤
≤α≤![]() ).
).

(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为α的函数;
(2)求y= 的最大值与最小值.
的最大值与最小值.
2007年
19.(本小题满分12分)
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次
烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根
据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率
依次为![]() ,
,![]() ,
,![]() ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依
次为![]() ,
,![]() ,
,![]() .
.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为![]() ,求随机变量
,求随机变量![]() 的期望.
的期望.
陕西卷(理)
2006年
(19)(本小题满分12分)
如图,![]() 点A在直线
点A在直线![]() 上的射影为
上的射影为![]() 点B在
点B在![]() 上的射影为
上的射影为![]()
已知![]() 求:
求:
(I)直线AB分别与平面![]() 所成角的大小;
所成角的大小;
(II)二面角![]() 的大小。
的大小。

(第19题图)
2007年
19.(本小题满分12分)
如图,在底面为直角梯形的四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() .
.![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.


四川卷(理)
2006年
(19)(本大题满分12分)
如图,在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,
![]() 分别是
分别是![]() 的中点,
的中点,![]()

(Ⅰ)求证:![]() 面
面![]() ;
;
(Ⅱ)求二面角![]() 的大小。
的大小。
2007年
(19)(本小题满分12分)如图,![]() 是直角梯形,∠
是直角梯形,∠![]() =90°,
=90°,![]() ∥
∥![]() ,
,
![]() =1,
=1,![]() =2,又
=2,又![]() =1,∠
=1,∠![]() =120°,
=120°,![]() ⊥
⊥![]() ,直线
,直线![]() 与直线
与直线![]() 所成
所成
的角为60°.
(Ⅰ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
安徽卷(理)
2006年
(19)(本小题满分12分)
如图,P是边长为1的正六边形ABCDDEF所在平面外一点,PA=1,P在平面ABC内的
射影为BF的中点O。

(Ⅰ)证明PA┴BF:
(Ⅱ)求面APB与面DPB所成二面角的大小。
2007年
18.(本小题满分14分)
设![]() ,
,![]() .
.
(Ⅰ)令![]() ,讨论
,讨论![]() 在
在![]() 内的单调性并求极值;
内的单调性并求极值;
(Ⅱ)求证:当![]() 时,恒有
时,恒有![]() .
.
海南宁夏卷(理)
2007年
19.(本小题满分12分)
在平面直角坐标系![]() 中,经过点
中,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个
有两个
不同的交点![]() 和
和![]() .
.
(I)求![]() 的取值范围;
的取值范围;
(II)设椭圆与![]() 轴正半轴、
轴正半轴、![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,是否存在常数
,是否存在常数![]() ,
,
使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。