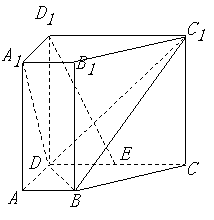
 如图,在直四棱柱
如图,在直四棱柱三、解答题
(19)(本小题满分12分)
 如图,在直四棱柱
如图,在直四棱柱![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)设![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
解法一:
 (Ⅰ)连结
(Ⅰ)连结![]() ,则四边形
,则四边形![]() 为正方形,
为正方形,
![]() ,且
,且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形.
为平行四边形.
![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
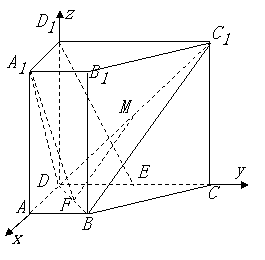
(Ⅱ)以![]() 为原点,
为原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示
轴建立如图所示
的空间直角坐标系,不妨设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
由![]() ,
,![]() ,
,
得
取![]() ,则
,则![]() .
.
又![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
由![]() ,
,![]() ,
,
得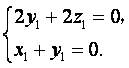
取![]() ,则
,则![]() ,
,
设![]() 与
与![]() 的夹角为
的夹角为![]() ,二面角
,二面角![]() 为
为![]() ,显然
,显然![]() 为锐角,
为锐角,
 .
.
 ,
,
即所求二面角![]() 的余弦为
的余弦为![]() .
.
解法二:
(Ⅰ)以![]() 为原点,
为原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图
轴建立如图
所示的空间直角坐标系,
设![]() ,由题意知:
,由题意知:

![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,
![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(Ⅱ)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,
由(Ⅰ)及题意得知:
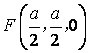 ,
,![]() ,
,
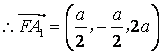 ,
,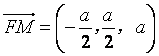 ,
,
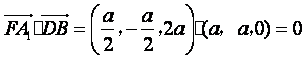 ,
,
 .
.
![]() ,
,![]() ,
,
![]() 为所求二面角的平面角.
为所求二面角的平面角.
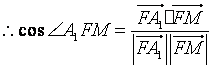
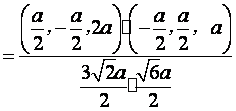
 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
解法三:
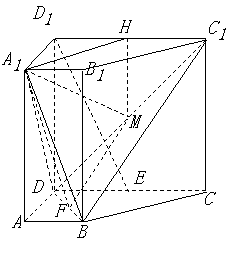 (Ⅰ)证明:如解法一图,连结
(Ⅰ)证明:如解法一图,连结![]() ,
,![]() ,
,
设![]() ,
,![]() ,连结
,连结![]() ,
,
由题意知![]() 是
是![]() 的中点,又
的中点,又![]() 是
是![]() 的中点,
的中点,
![]() 四边形
四边形![]() 是平行四边形,故
是平行四边形,故![]() 是
是![]() 的中点,
的中点,
![]() 在
在![]() 中,
中,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(Ⅱ)如图,在四边形![]() 中,设
中,设![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
故![]() ,由(Ⅰ)得
,由(Ⅰ)得
![]() ,
,![]() ,
,
![]() ,即
,即![]() .
.
又![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() ,
,
取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,
由题意知:![]() ,
,
![]() .
.
又![]() ,
,![]() .
.
![]() 为二面角
为二面角![]() 的平面角.
的平面角.
连结![]() ,在
,在![]() 中,
中,
由题意知:
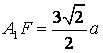 ,
, ,
,
取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,
在![]() 中,
中,
![]() ,
,![]() ,
,
![]() .
.
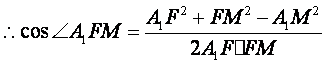

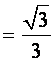 .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。