三、解答题
19.(本小题满分12分)
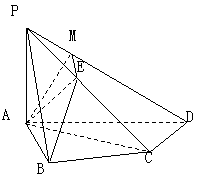
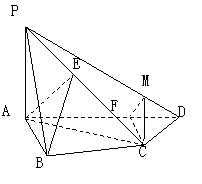
如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,
![]() ,
,![]() 是
是![]() 的中点.
的中点.
 (Ⅰ)证明
(Ⅰ)证明![]() ;
;
(Ⅱ)证明![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
本小题考查直线与直线垂直、直线与平面垂直、二面角等基础知识,考查空间想象
能力、运算能力和推理论证能力.满分12分.
(Ⅰ)证明:在四棱锥![]() 中,因
中,因![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,故
,故![]() .
.
![]() ,
,![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,
,![]() .
.
(Ⅱ)证明:由![]() ,
,![]() ,可得
,可得![]() .
.
![]() 是
是![]() 的中点,
的中点,![]() .
.
由(Ⅰ)知,![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,
,![]() .
.
![]() 底面
底面![]() 在底面
在底面![]() 内的射影是
内的射影是![]() ,
,![]() ,
,![]() .
.
又![]() ,综上得
,综上得![]() 平面
平面![]() .
.
(Ⅲ)解法一:过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .则(Ⅱ)知,
.则(Ⅱ)知,
![]() 平面
平面![]() ,
,![]() 在平面
在平面![]() 内的射影是
内的射影是![]() ,则
,则![]() .
.
因此![]() 是二面角
是二面角![]() 的平面角.
的平面角.
由已知,得![]() .设
.设![]() ,
,
可得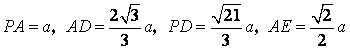 .
.
在![]() 中,
中,![]() ,
,![]() ,
,
 则
则 .
.
在![]() 中,
中,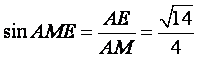 .
.
所以二面角![]() 的大小是
的大小是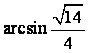 .
.
解法二:由题设![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() ,交线为
,交线为![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,故
,故![]() 平面
平面![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
连结![]() ,故
,故![]() .因此
.因此![]() 是二面角
是二面角![]() 的平面角.
的平面角.
由已知,可得![]() ,设
,设![]() ,
,
可得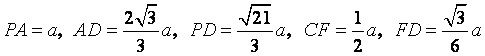 .
.
![]() ,
,![]() .
.
于是, .
.
在![]() 中,
中,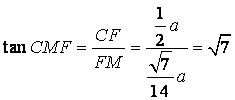 .
.
所以二面角![]() 的大小是
的大小是![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。