三、解答题
(19)(本小题满分12分)
如图,l1、l2是互相垂直的异面直线,MN是它们的公垂线段,点A、B在l1上,C在
l2上,AM=MB=MN。
(Ⅰ)证明![]() ;
;
(Ⅱ)若![]() ,求NB与平面ABC所成角的余弦值。
,求NB与平面ABC所成角的余弦值。
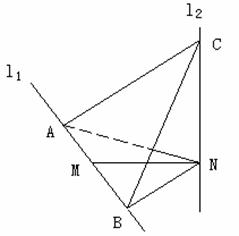
解法一:
(Ⅰ)由已知![]() ,
,![]() ,可得
,可得![]() 平面
平面![]() 由已知
由已知![]() ,
,
可知![]() 且
且![]() ,又
,又![]() 为
为![]() 在平面
在平面![]() 内的射影,
内的射影,
![]()
(Ⅱ)![]() ,
,
![]() ,又已知
,又已知![]() ,因此
,因此![]() 为正三角形.
为正三角形.
![]() ,
,
![]() ,因此
,因此![]() 在平面
在平面![]() 内的射影
内的射影![]() 是正三角形
是正三角形![]() 的中心,连结
的中心,连结![]() ,
,
![]() 为NB与平面
为NB与平面![]() 所成的角.
所成的角.
在![]() 中,
中,

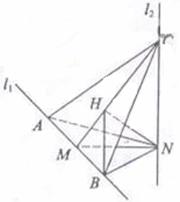
解法二:
如图,建立空间直角坐标系![]() 令
令![]() ,
,
则有![]() ,
,![]() ,
,![]()
(Ⅰ)![]() 是
是![]() 、
、![]() 的公垂线,
的公垂线,![]() ,
,
![]() 平面
平面![]()
![]() 平行于
平行于![]() 轴
轴
故可设![]()
于是![]() ,
,
![]() ,
,
![]()
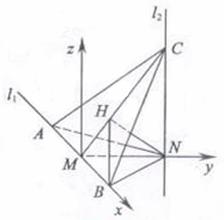
(Ⅱ)![]() ,
,
又已知![]() ,
,![]() 为正三角形,
为正三角形,![]()
在![]() 中,
中,![]() ,可得
,可得![]() ,故
,故![]()
连接![]() ,作
,作![]() 于
于![]() ,设
,设![]()
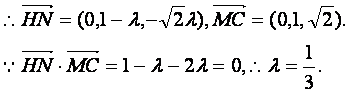
 ,可得
,可得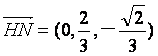 ,连结
,连结![]() ,则
,则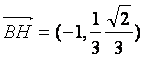 ,
,
![]() ,
,![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,
,![]() 为
为![]() 与平面
与平面![]() 所成的角
所成的角
又![]() ,
,

本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。