一、解答题

(19) (本小题满分12分)

现有甲、乙两个项目，对甲项目每投资十万元，一年后利润是1.2万元、1.18万元、

1.17万元的概率分别为、、;已知乙项目的利润与产品价格的调整有关,在每

次调整中,价格下降的概率都是,设乙项目产品价格在一年内进行2次独立

后相应利润是1.3万元、1.25万元、0.2万元.随机变量、分别表示对甲、乙两

项目各投资十万元一年后的利润.

( = 1 \* ROMAN I)  求、的概率分布和数学期望、;

( = 2 \* ROMAN II)  当时,求的取值范围.

本小题主要考查二项分布、分布列、数学期望等基础知识，考查学生运用概率知识解

决实际问题的能力.满分12分.

(Ⅰ)解法一：ξ₁的概率分布为

Eξ₁=1.2×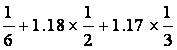

=1.18.

由题设得ξ-B（2，p），即ξ的概率分布为

故ξ₂的概率分而为

所以ξ₂的数学期望为

Eξ₂=1.3×(1-p)²+1.25×2p(1-p)+0.2×p²

      =1.3×(1-2p+p²)+2.5×(p-p²)+0.2×p²

      =-p²-0.1p+1.3.

解法二：ξ₁的概率分布为

Eξ₁=1.2×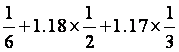

    =1.18.

设A_i表示事件“第1次调整，价格下降”（i=1，2），则

P（ξ=0）=P（₁）P（₂）=（1-p）²，

P（ξ=1）=P（A₁）P（₂）+P（₁）P（A₂）

         =2p（1-p）

P（ξ=2）=P（A₁）P（A₂）=p².

故ξ₂的概率分布为

所以ξ₂的数学期望为

Eξ₂=1.3×(1-p)²+1.25×2p(1-p)+0.2×p²

    =1.3×(1-2p+p²)+2.5×(p-p²)+0.2×P²

     = -p²-0.1p+1.3.

(Ⅱ)解：由Eξ₁＜Eξ₂，得

-p²-0.1p+1.3＞1.18.

整理得

（p+0.4）(p-0.3)＜0,

解得

-0.4＜p＜0.3.

因为0＜p＜1,所以，当Eξ₁＜Eξ₂时，p的取值范围是

0＜p＜0.3.