福建(理)
选择题
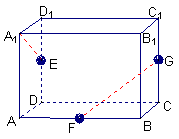
8.如图,长方体ABCD—A1B1C1D1中,AA1=AB=2,
AD=1,点E、F、G分别是DD1、AB、CC1的中

点,则异面直线A1E与GF所成的角是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
解答题
20.(本小题满分12分)
如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,
F为CE上的点,且BF⊥平面ACE.
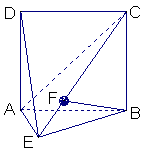 (Ⅰ)求证AE⊥平面BCE;
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B—AC—E的大小;
(Ⅲ)求点D到平面ACE的距离.
浙江(理)
选择题(每小题5分)
6.设![]() 、
、![]() 为两个不同的平面,l、m为两条不同的直线,且l
为两个不同的平面,l、m为两条不同的直线,且l![]()
![]() ,m
,m![]()
![]() ,
,
有如下的两个命题:①若![]() ∥
∥![]() ,则l∥m;②若l⊥m,则
,则l∥m;②若l⊥m,则![]() ⊥
⊥![]() .那么
.那么
(A) ①是真命题,②是假命题 (B) ①是假命题,②是真命题
(C) ①②都是真命题 (D) ①②都是假命题
填空题(每小题4分)
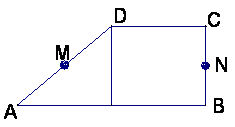
12.设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,
使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线
与AE所成角的大小等于_________.
解答题
18.如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,
OP⊥底面ABC.
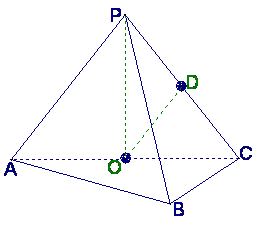 (Ⅰ)当k=
(Ⅰ)当k=![]() 时,求直线PA与平面PBC所成角的大小;
时,求直线PA与平面PBC所成角的大小;
(Ⅱ) 当k取何值时,O在平面PBC内的射影恰好
为△PBC的重心?
天津(理)
选择题(每小题5分)
(4)设![]() 为平面,
为平面,![]() 为直线,则
为直线,则![]() 的一个充分条件是( )
的一个充分条件是( )
(A)
![]() (B)
(B)
![]()
(C)
![]() (D)
(D)
![]()
填空题(每小题4分)
(12)如图,PA⊥平面ABC,∠ACB=90°且PA=AC=BC=a则异面
直线PB与AC所成角的正切值等于________.

解答题
(19)(本小题满分12分)
如图,在斜三棱柱![]() 中,
中,![]() ,
,
侧面![]() 与底面ABC所成的二面角为
与底面ABC所成的二面角为![]() ,E、F分别是棱
,E、F分别是棱![]() 的中点
的中点
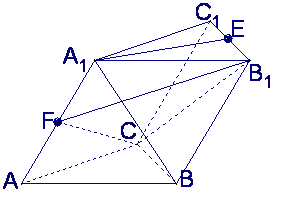 (Ⅰ)求
(Ⅰ)求![]() 与底面ABC所成的角
与底面ABC所成的角
(Ⅱ)证明![]() ∥平面
∥平面![]()
(Ⅲ)求经过![]() 四点的球的体积
四点的球的体积
江苏
选择题(每小题5分)
4.在正三棱柱![]() 中,若AB=2,
中,若AB=2,![]() 则点A到平面
则点A到平面![]() 的距离为(
)
的距离为(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解答题
21.(本小题满分14分,第一小问满分6分,第二.第三小问满分各4分)
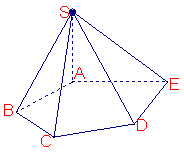 如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,
如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,![]() ,
,
![]()
![]()
⑴求异面直线CD与SB所成的角(用反三角函数值表示);
⑵证明:BC⊥平面SAB;
⑶用反三角函数值表示二面角B—SC—D的大小![]() (本小问不必写出解答过程)
(本小问不必写出解答过程)
辽宁
选择题(每小题5分)
4.已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出
下列四个命题:
①若![]() ;
;
②若![]() ;
;
③若![]() ;
;
④若m、n是异面直线,![]()
其中真命题是( )
A.①和② B.①和③ C.③和④ D.①和④
填空题(每小题4分)
14.如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,
那么点M到截面ABCD的距离是 .
解答题
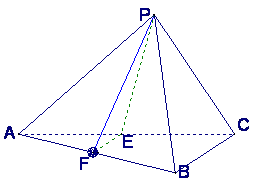 17.(本小题满分12分)
17.(本小题满分12分)
已知三棱锥P—ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
(Ⅰ)证明PC⊥平面PAB;
(Ⅱ)求二面角P—AB—C的平面角的余弦值;
(Ⅲ)若点P、A、B、C在一个表面积为12π的
球面上,求△ABC的边长.
重庆(理)
选择题(每小题5分)
7.对于不重合的两个平面![]() 与
与![]() ,给定下列条件:
,给定下列条件:
①存在平面![]() ,使得
,使得![]() 、
、![]() 都垂直于
都垂直于![]() ;
;
②存在平面![]() ,使得
,使得![]() 、
、![]() 都平行于
都平行于![]() ;
;
③![]() 内有不共线的三点到
内有不共线的三点到![]() 的距离相等;
的距离相等;
④存在异面直线l、m,使得l//![]() ,l//
,l//![]() ,m//
,m//![]() ,m//
,m//![]() ,
,
其中,可以判定![]() 与
与![]() 平行的条件有(
)
平行的条件有(
)
A.1个 B.2个 C.3个 D.4个
10.如图,在体积为1的三棱锥A—BCD侧棱AB、AC、AD上分别取点E、F、G,
使AE : EB=AF : FC=AG : GD=2 : 1,
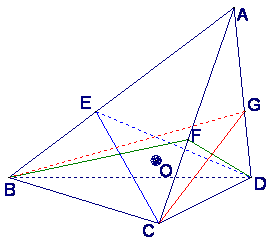
记O为三平面BCG、CDE、DBF的交点,
则三棱锥O—BCD的体积等于 ( )
A.![]() B.
B.![]()
C. ![]() D.
D.![]()
20.(本小题满分13分)
如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,
EA⊥EB1,已知AB=![]() ,BB1=2,BC=1,∠BCC1=
,BB1=2,BC=1,∠BCC1=![]() ,求:
,求:
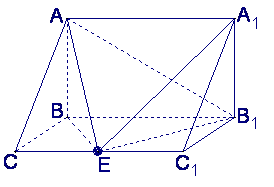 (Ⅰ)异面直线AB与EB1的距离;
(Ⅰ)异面直线AB与EB1的距离;
(Ⅱ)二面角A—EB1—A1的平面角的正切值.
湖南(理)
选择题(每小题5分)
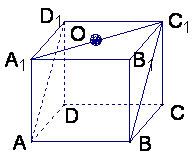 5.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,
5.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,
则O到平面AB C1D1的距离为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
解答题
17.(本题满分12分)
如图1,已知ABCD是上.下底边长分别为2和6,高为![]() 的等腰梯形,
的等腰梯形,
将它沿对称轴OO1折成直二面角,如图2.
(Ⅰ)证明:AC⊥BO1;
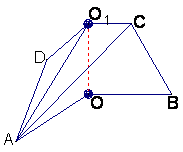
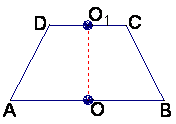
(Ⅱ)求二面角O-AC-O1的大小.
解答 图1
湖北(理)选择题(每小题5分)
10.如图,在三棱柱![]() 中,点E、F、H、K分别为
中,点E、F、H、K分别为![]() 、
、![]() 、
、![]() 、
、![]()
的中点,G为ΔABC的重心![]() 从K、H、G、
从K、H、G、![]() 中取一点作为P,使得该棱柱恰有2条棱
中取一点作为P,使得该棱柱恰有2条棱
与平面PEF平行,则P为
A.K B.H
C.G
D.![]()
解答题
20.(本小题满分12分)
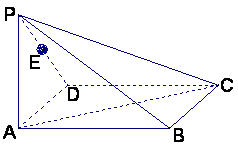 如图,在四棱锥P—ABC右,底面ABCD为矩形,侧棱PA⊥底面ABCD,
如图,在四棱锥P—ABC右,底面ABCD为矩形,侧棱PA⊥底面ABCD,
AB=![]() ,BC=1,PA=2,E为PD的中点
,BC=1,PA=2,E为PD的中点![]()
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,
并求出N点到AB和AP的距离![]()
广东
选择题(每小题5分)
4.已知高为3的直棱柱ABC—A′B′C′的底面是边长为1的正三
角形(如图1所示),则三棱锥B′—ABC的体积为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.给出下列关于互不相同的直线m、l、n和平面α、β的四个命题:
①若![]() ;
;
②若m、l是异面直线,![]() ;
;
③若![]() ;
;
④若![]()
其中为假命题的是
A.① B.② C.③ D.④
解答题
16.(本小题满分14分)
如图3所示,在四面体P—ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=![]() .
.
F是线段PB上一点,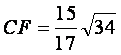 ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.
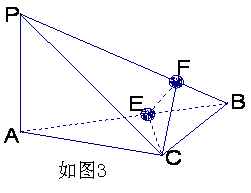 (Ⅰ)证明:PB⊥平面CEF;
(Ⅰ)证明:PB⊥平面CEF;
(Ⅱ)求二面角B—CE—F的大小.
北京(理)
选择题(每小题5分)
(6)在正四面体P—ABC中,D,E,F分别是AB,BC,CA的中点,
下面四个结论中不成立的是
(A)BC∥平面PDF
(B)DF![]() 平面PAE
平面PAE
(C)平面PDF![]() 平面ABC
(D)平面PAE
平面ABC
(D)平面PAE![]() 平面ABC
平面ABC
解答题
(16)(本小题共14分)
如图,在直四棱柱![]() 中,
中,![]() ,
,
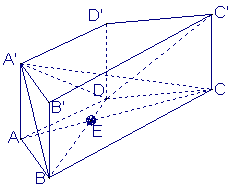
![]() 垂足为
垂足为![]()
![]()
(Ⅰ)求证![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求异面直线![]() 与
与![]() 所成角的大小
所成角的大小![]()
上海(理)
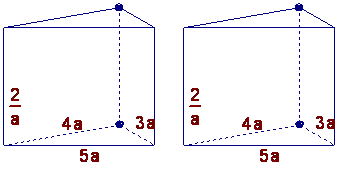
填空题(每小题4分)
11.有两个相同的直三棱柱,高为![]() ,底面三角形的三边长分别为
,底面三角形的三边长分别为![]() 、
、![]() 、
、![]()
![]()
![]()
用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的一个是四棱柱,
则![]() 的取值范围是_______
的取值范围是_______![]()
解答题
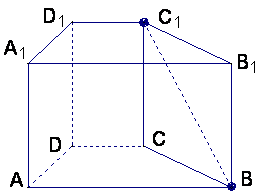
17.已知直四棱柱![]() 中,
中,![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求异面直线
,求异面直线![]() 与
与![]()
所成的角的大小![]() (结果用反三角函数表示)
(结果用反三角函数表示)
山东(理)
选择题(每小题5分)
(8)设地球半径为R,若甲地位于北纬![]() 东经
东经![]() ,乙地位于南纬度
,乙地位于南纬度![]() 东经
东经![]() ,
,
则甲、乙两地球面距离为
(A)![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(16)已知m、n是不同的直线,![]() 是不重合的平面,给出下列命题:
是不重合的平面,给出下列命题:
①若![]() 则
则![]()
![]()
②若![]() 则
则![]()
![]()
③若![]() ,则
,则![]()
![]()
④m、n是两条异面直线,若![]() 则
则![]()
![]()
上面命题中,真命题的序号是____________(写出所有真命的序号)![]()
解答题
 (20)
(本小题满分12分)
(20)
(本小题满分12分)
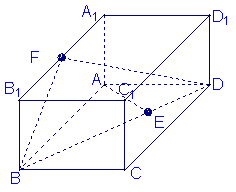
如图,已知长方体![]()
![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]()
所成的角为![]() ,
,![]() 垂直
垂直![]() 于
于![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角(锐角)的大小;
所成二面角(锐角)的大小;
(Ⅲ)求点![]() 到平面
到平面![]() 的距离
的距离![]()
江西(理)
选择题(每小题5分)
9.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,
则四面体ABCD的外接球的体积为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
填空题(每小题4分)
15.如图,在直三棱柱ABC—A1B1C1中,AB=BC=![]() ,BB1=2,
,BB1=2,![]() ,E、F
,E、F
分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为 .
解答题
20.(本小题满分12分)
如图,在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
 (3)AE等于何值时,二面角D1—EC—D的大小为
(3)AE等于何值时,二面角D1—EC—D的大小为![]() .
.
全国卷(Ⅰ)理
选择题(每小题5分)
(3)一个与球心距离为1的平面截球所得的圆面面积为![]() ,则球的表面积为
,则球的表面积为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
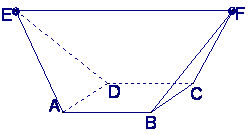
(5)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且![]()
均为正三角形,EF∥AB,EF=2,则该多面体的体积为
 (A)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(12)过三棱柱任意两个顶点的直线共15条,其中异面直线有
(A)18对 (B)24对 (C)30对 (D)36对
填空题(每小题4分)
(16)在正方形![]() 中,过对角线
中,过对角线![]() 的一个平面交
的一个平面交![]() 于E,交
于E,交![]() 于F,则
于F,则
①
四边形![]() 一定是平行四边形
一定是平行四边形
②
四边形![]() 有可能是正方形
有可能是正方形
③
四边形![]() 在底面ABCD内的投影一定是正方形
在底面ABCD内的投影一定是正方形
④
四边形![]() 有可能垂直于平面
有可能垂直于平面![]()
以上结论正确的为 ![]() (写出所有正确结论的编号)
(写出所有正确结论的编号)
解答题
(18)(本大题满分12分)
 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,![]() 底面ABCD,
底面ABCD,
且PA=AD=DC=![]() AB=1,M是PB的中点
AB=1,M是PB的中点![]()
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小![]()
全国卷(Ⅱ)理
选择题(每小题5分)
(2)正方体![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点.
的中点.
那么,正方体的过![]() 、
、![]() 、
、![]() 的截面图形是
的截面图形是
(A)三角形 (B)四边形 (C)五边形 (D)六边形
(12)将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面
体的高的最小值为
(A) (B)2+
(B)2+![]() (C)4+
(C)4+![]() (D)
(D)
填空题(每小题5分)
(16)下面是关于三棱锥的四个命题:
①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥.
④侧棱与底面所成的角相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
其中,真命题的编号是_____________.(写出所有真命题的编号)
解答题
(20)(本小题满分12分)
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD,E、F分别
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD,E、F分别
为CD、PB的中点.
(Ⅰ)求证:EF垂直于平面PAB;
(Ⅱ)设AB=![]() BC,求AC与平面AEF所成的角的大小.
BC,求AC与平面AEF所成的角的大小.
全国卷(Ⅲ)理
选择题(每小题5分)
4.设三棱柱ABC-A1B1C1的体积是V,P.Q分别是侧棱AA1.CC1上的点,且PA=QC1,
则四棱锥B-APQC的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.不共面的四个定点到平面α的距离都相等,这样的平面α共有( )个
A.3 B.4 C.6 D.7
解答题
18.(本小题满分12分)
四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,
平面VAD⊥底面ABCD![]()
 1)求证AB⊥面VAD;
1)求证AB⊥面VAD;
2)求面VAD与面VDB所成的二面角的大小.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。