解答题

     17．（本小题满分12分）

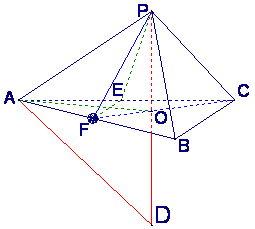
 已知三棱锥P—ABC中，E、F分别是AC、AB的中点,△ABC，△PEF都是正三角形，PF⊥AB.

    （Ⅰ）证明PC⊥平面PAB；

    （Ⅱ）求二面角P—AB—C的平面角的余弦值；

    （Ⅲ）若点P、A、B、C在一个表面积为12π的

         球面上，求△ABC的边长.

本小题主要考查空间中的线面关系，三棱锥、球的有关概念及解三角形等基础知识，

考查空间想象能力及运用方程解未知量的基本方法，满分12分.

（Ⅰ）证明： 连结CF.

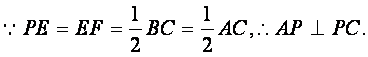
……4分

（Ⅱ）解法一：

为所求二面角的平面角. 设AB=a，则AB=a，则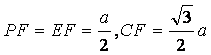

……………………8分

解法二：设P在平面ABC内的射影为O. ≌≌

得PA=PB=PC. 于是O是△ABC的中心. 为所求二面角的平面角.

设AB=a，则   ………8分

（Ⅲ）解法一：设PA=x，球半径为R.

，的边长为.……12分

解法二：延长PO交球面于D，那么PD是球的直径.

连结OA、AD，可知△PAD为直角三角形.  设AB=x，球半径为R.

.……12分