解答题
17.已知直四棱柱![]() 中,
中,![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求异面直线
,求异面直线![]() 与
与![]()
所成的角的大小![]() (结果用反三角函数表示)
(结果用反三角函数表示)
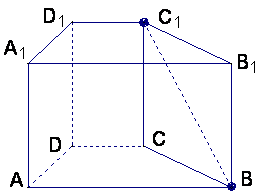
[解]由题意AB∥CD,∴∠C1BA是异面直线BC1与DC 所成的角.连结AC1与AC,
在Rt△ADC中,可得AC=![]() .
又在Rt△ACC1中,可得AC1=3.
.
又在Rt△ACC1中,可得AC1=3.
在梯形ABCD中,过C作CH∥AD交AB于H,
得∠CHB=90°,CH=2,HB=3, ∴CB=![]() .
.

又在Rt△CBC1中,可得BC1=![]() ,
,
在△ABC1中,cos∠C1BA=![]() ,∴∠C1BA=arccos
,∴∠C1BA=arccos![]()
 异面直线BC1与DC所成角的大小为arccos
异面直线BC1与DC所成角的大小为arccos![]()
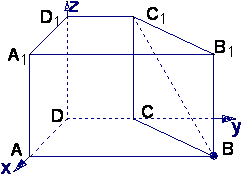
另解:如图,以D为坐标原点,分别以DA、DC、DD1所在
直线为x、y、z轴建立直角坐标系.
则C1(0,1,2),B(2,4,0), ∴![]() =(-2,-3,2),
=(-2,-3,2),
![]() =(0,-1,0),设
=(0,-1,0),设![]() 与
与![]() 所成的角为θ,
所成的角为θ,
则cosθ=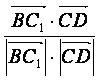 =
=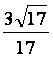 ,θ=
arccos
,θ=
arccos .
.
异面直线BC1与DC所成角的大小为arccos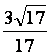
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。