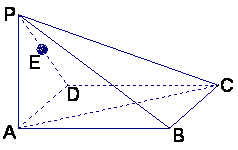
 如图,在四棱锥P—ABC右,底面ABCD为矩形,侧棱PA⊥底面ABCD,
如图,在四棱锥P—ABC右,底面ABCD为矩形,侧棱PA⊥底面ABCD,解答题
20.(本小题满分12分)
 如图,在四棱锥P—ABC右,底面ABCD为矩形,侧棱PA⊥底面ABCD,
如图,在四棱锥P—ABC右,底面ABCD为矩形,侧棱PA⊥底面ABCD,
AB=![]() ,BC=1,PA=2,E为PD的中点
,BC=1,PA=2,E为PD的中点![]()
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,
并求出N点到AB和AP的距离![]()
解:
解法一:(Ⅰ)建立如图所示的空间直角坐标系,
则A、B、C、D、P、E的坐标分别为A(0,0,0),
B(![]() ,0,0),C(
,0,0),C(![]() ,1,0),D(0,1,0),
,1,0),D(0,1,0),
P(0,0,2),E(0,![]() ,2)
,2)![]()
从而![]() =(
=(![]() ,1,0),
,1,0),![]() =(
=(![]() ,0,-2)
,0,-2)![]()
设![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则
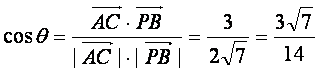 ,
,
∴AC与PB所成角的余弦值为![]()
![]()
(Ⅱ)由于N点在侧面PAB内,故可设N点坐标为(x,0,z),
则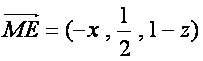
![]()
 由NE⊥面PAC可得:
由NE⊥面PAC可得: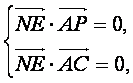 即
即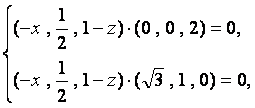
化简得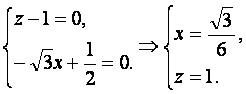
即N点的坐标为(![]() ,0,1),从而N点到AB、AP的距离分别为1,
,0,1),从而N点到AB、AP的距离分别为1,![]()
![]()
解法二:(Ⅰ)设AC∩BD=O,连OE,则OE//PB,
∴∠EOA即为AC与PB所成的角或其补角![]()
在ΔAOE中,AO=1,OE=![]() PB=
PB=![]() ,AE=
,AE=![]() PD=
PD=![]() ,
,
∴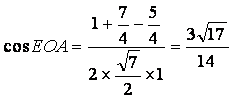
![]()
即AC与PB所成角的余弦值为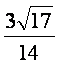
![]()
(Ⅱ)在面ABCD内过D作AC的垂线交AB于F,则
![]()
连PF,则在RtΔADF中DF=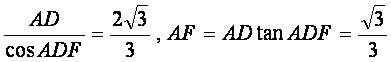
![]()
设N为PF的中点,连NE,则NE//DF,
∵DF⊥AC,DF⊥PA,∴DF⊥面PAC![]() 从而NE⊥面PAC
从而NE⊥面PAC![]()
∴N点到AB的距离=![]() AP=1,N点到AP的距离=
AP=1,N点到AP的距离=![]() AF=
AF=![]()
![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。