 (3)AE等于何值时,二面角D1—EC—D的大小为
(3)AE等于何值时,二面角D1—EC—D的大小为解答题
20.(本小题满分12分)
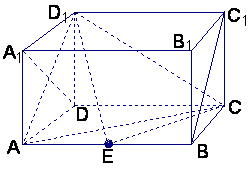
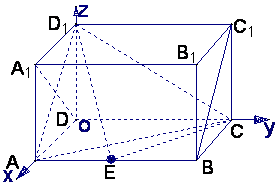
如图,在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
 (3)AE等于何值时,二面角D1—EC—D的大小为
(3)AE等于何值时,二面角D1—EC—D的大小为![]() .
.
解法(一)
(1)证明:∵AE⊥平面AA1DD1,A1D⊥AD1,∴A1D⊥D1E
(2)设点E到面ACD1的距离为h,在△ACD1中,AC=CD1=![]() ,AD1=
,AD1=![]() ,
,
故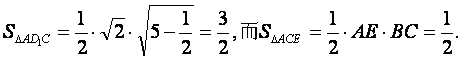
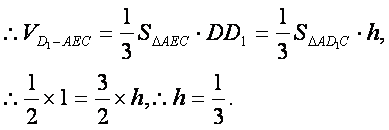
(3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,
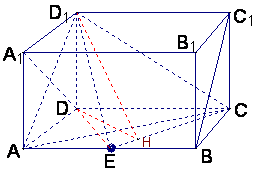 ∴∠DHD1为二面角D1—EC—D的平面角.
∴∠DHD1为二面角D1—EC—D的平面角.
设AE=x,则BE=2-x
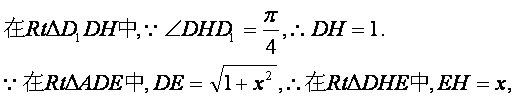
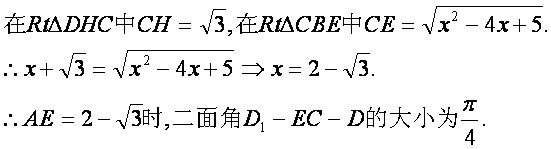
解法(二):以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立
空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),
E(1,x,0),A(1,0,0)C(0,2,0)
(1)![]()
(2)因为E为AB的中点,则E(1,1,0),
 从而
从而![]() ,
,
![]() ,
,
设平面ACD1的法向量为![]() ,
,
则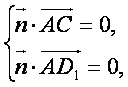
也即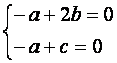 ,得
,得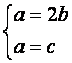 ,从而
,从而![]() ,所以点E到平面AD1C的距离为
,所以点E到平面AD1C的距离为
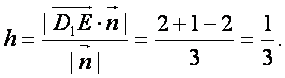
(3)设平面D1EC的法向量![]() ,
,
∴![]()
由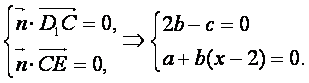 令b=1, ∴c=2,a=2-x,
令b=1, ∴c=2,a=2-x,
∴![]()
依题意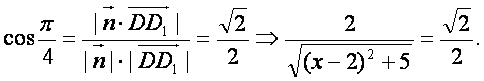
∴![]() (不合,舍去),
(不合,舍去),![]() .
.
∴AE=![]() 时,二面角D1—EC—D的大小为
时,二面角D1—EC—D的大小为![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。