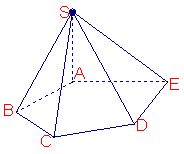
 如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,
如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,解答题
21.(本小题满分14分,第一小问满分6分,第二.第三小问满分各4分)
 如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,
如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,![]() ,
,
![]()
![]()
⑴求异面直线CD与SB所成的角(用反三角函数值表示);
⑵证明:BC⊥平面SAB;
⑶用反三角函数值表示二面角B—SC—D的大小![]() (本小问不必写出解答过程)
(本小问不必写出解答过程)
 (21)(Ⅰ)连结BE,延长BC、ED交于点F,则∠DCF=∠CDF=600,
(21)(Ⅰ)连结BE,延长BC、ED交于点F,则∠DCF=∠CDF=600,
∴△CDF为正三角形,∴CF=DF![]()
又BC=DE,∴BF=EF![]() 因此,△BFE为正三角形,
因此,△BFE为正三角形,
∴∠FBE=∠FCD=600,∴BE//CD
所以∠SBE(或其补角)就是异面直线CD与SB所成的角![]()
∵SA⊥底面ABCDE,SA=AB=AE=2,
∴SB=![]() ,同理SE=
,同理SE=![]() ,
,
又∠BAE=1200,所以BE=![]() ,从而,cos∠SBE=
,从而,cos∠SBE=![]() ,
,
∴∠SBE=arccos![]()
![]()
所以异面直线CD与SB所成的角是arccos![]()
![]()
(Ⅱ) 由题意,△ABE为等腰三角形,∠BAE=1200,
∴∠ABE=300,又∠FBE =600,
∴∠ABC=900,∴BC⊥BA
∵SA⊥底面ABCDE,BC![]() 底面ABCDE,
底面ABCDE,
∴SA⊥BC,又SA![]() BA=A,
BA=A,
∴BC⊥平面SAB![]()
(Ⅲ)二面角B-SC-D的大小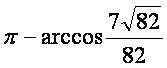
![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。