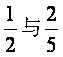 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.福建(理)
解答题
18.(本小题满分12分)
甲、乙两人在罚球线投球命中的概率分别为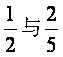 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.
(Ⅰ)甲、乙两人在罚球线各投球一次,求两人得分之和ξ的数学期望;
(Ⅱ)甲、乙两人在罚球线各投球二次,求这四次投球中至少一次命中的概率;
浙江(理)
解答题
19.袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是![]() ,
,
从B中摸出一个红球的概率为p.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.(i)求恰好
摸5次停止的概率;(ii)记5次之内(含5次)摸到红球的次数为![]() ,求随机变量
,求随机变量![]() 的
的
分布率及数学期望E![]() .
.
(Ⅱ) 若A、B两个袋子中的球数之比为12,将A、B中的球装在一起后,从中摸
出一个红球的概率是![]() ,求p的值.
,求p的值.
天津(理)
选择题(每小题4分)
(7)某人射击一次击中的概率为0.6,经过3次射击,此人至少有两次击中目标的概率为()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
填空题(每小题4分)
(15)某公司有5万元资金用于投资开发项目,如果成功,一年后可获利12%,一旦失
败,一年后将丧失全部资金的50%,下表是过去200例类似项目开发的实施结果:
|
投资成功 |
投资失败 |
|
192次 |
8次 |
则该公司一年后估计可获收益的期望是___________(元)
江苏
解答题
20.(本小题满分12分,每小问满分4分)甲.乙两人各射击一次,
击中目标的概率分别是![]() 和
和![]()
![]() 假设两人射击是否击中目标,相互之间没有影响;
假设两人射击是否击中目标,相互之间没有影响;
每人各次射击是否击中目标,相互之间也没有影响![]()
⑴求甲射击4次,至少1次未击中目标的概率;
⑵求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
⑶假设某人连续2次未击中目标,则停止射击![]() 问:乙恰好射击5次后,被中止
问:乙恰好射击5次后,被中止
射击的概率是多少?
辽宁
选择题(每小题5分)
3.设袋中有80个红球,20个白球,若从袋中任取10个球,则其中恰有
6个红球的概率为( )
A.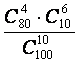 B.
B.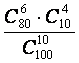 C.
C.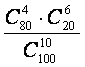 D.
D.
解答题
20.(本小题满分12分)
某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序加工而成,
两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级.对
每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品.
(Ⅰ)已知甲、乙两种产品每一道工序的加工结

果为A级的概率如表一所示,分别求生产
出的甲、乙产品为一等品的概率P甲、P乙;
(Ⅱ)已知一件产品的利润如表二所示,用ξ、
η分别表示一件甲、乙产品的利润,在
(I)的条件下,求ξ、η的分布列及
Eξ、Eη;
(Ⅲ)已知生产一件产品需用的工人数和资金额
如表三所示.该工厂有工人40名,可用资
金60万元.设x、y分别表示生产甲、乙产品的数量,在(II)的条件下,x、y为何
值时,![]() 最大?最大值是多少?
最大?最大值是多少?
(解答时须给出图示)
重庆(理)
填空题(每小题4分)
15.某轻轨列车有4节车厢,现有6位乘客准备乘坐,设每一位乘客进入每节
车厢是等可能的,则这6位乘客进入各节车厢的人数恰好为0,1,2,3的概
率为
![]()
解答题
18.(本小题满分13分)
在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;
有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券
中任抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值![]() (元)的概率分布列和期望
(元)的概率分布列和期望![]()
![]()
湖南(理)
解答题
18.(本小题满分14分)
某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别
是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开
该城市时游览的景点数与没有游览的景点数之差的绝对值.
(Ⅰ)求ξ的分布及数学期望;
(Ⅱ)记“函数f(x)=x2-3ξx+1在区间[2,+∞![]() 上单调递增”为
上单调递增”为
事件A,求事件A的概率.
湖北(理)
选择题(每小题5分)
11.某初级中学有学生270人,其中一年级108人,二、三年级各81人,
现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层
抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、
二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一
随机编号为1,2,…,270,并将整个编号依次分为10段,如果抽得号码有
下列四种情况:
①7,34,61,88,115,142,169,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30![]() 57
57![]() 84
84![]() 111
111![]() 138
138![]() 165
165![]() 192
192![]() 219
219![]() 246
246![]() 270
270![]()
关于上述样本的下列结论中,正确的是
A.②、③都不能为系统抽样 B.②、④都不能为分层抽样
C.①、④都可能为系统抽样 D.①、③都可能为分层抽样
12.以平行六面体![]() 的任意三个顶点为顶点作三角形,从中随机
的任意三个顶点为顶点作三角形,从中随机
取出两个三角形,则这两个三角形不共面的概率p为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解答题
19.(本小题满分12分)
某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有4次参加
考试的机会,一量某次考试通过,便可领取驾照,不再参加以后的考试,否则
就一直考到第4次为止![]() 如果李明决定参加驾照考试,设他每次参加考试通过的
如果李明决定参加驾照考试,设他每次参加考试通过的
概率依次为0.6,0.7,0.8,0.9![]() 求在一年内李明参加驾照考试次数
求在一年内李明参加驾照考试次数![]() 的分布列
的分布列
和![]() 的期望,并求李明在一所内领到驾照的概率
的期望,并求李明在一所内领到驾照的概率
广东
选择题(每小题5分)
8.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、
5、6),骰子朝上的面的点数分别为X、Y,则![]() 的概率为(
)
的概率为(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解答题
18.(本小题满分12分)
箱中装有大小相同的黄、白两种颜色的乒乓球,黄、白乒乓球的数量比为s:t.
现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则
将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过n次,
以ξ表示取球结束时已取到白球的次数.
(Ⅰ)求ξ的分布列;
(Ⅱ)求ξ的数学期望.
北京(理)
解答题
(17)(本小题共13分)
甲、乙俩人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]()
![]()
(Ⅰ)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望
的概率分布及数学期望![]() ;
;
(Ⅱ)求乙至多击中目标2次的概率;
(Ⅲ)求甲恰好比乙多击中目标2次的概率![]()
上海(理)
填空题(每小题4分)
8.某班有50名学生,其15人选修A课程,另外35人选修B课程![]() 从班级中任选两名学生,
从班级中任选两名学生,
他们是选修不同课程的学生的概率是____________![]() (结果用分数表示)
(结果用分数表示)
山东(理)
选择题(每小题5分)
(9)10张奖券中只有3张有奖,5个人购买,每人1张,至少有1人中奖的概率是
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)![]()
解答题
(18) (本小题满分12分)
袋中装有罴球和白球共7个,从中任取2个球都是白球的概率为![]() .现有甲、乙
.现有甲、乙
两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取![]() 取后不放回,
取后不放回,
直到两人中有一人取到白球时即终止![]() 每个球在每一次被取出的机会是等可能的,
每个球在每一次被取出的机会是等可能的,
用![]() 表示取球终止时所需的取球次数.
表示取球终止时所需的取球次数.
![]() (Ⅰ)求袋中原有白球的个数;
(Ⅰ)求袋中原有白球的个数;
(Ⅱ)求随机变量![]() 的概率分布;
的概率分布;
(Ⅲ)求甲取到白球的概率![]()
江西(理)
选择题(每小题5分)
12.将1,2,…,9这9个数平均分成三组,则每组的三个数都成等差
数列的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解答题
19.(本小题满分12分)
A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面
朝上时A赢得B一张卡片,否则B赢得A一张卡片.规定掷硬币的次数达9次时,或
在此前某人已赢得所有卡片时游戏终止.设![]() 表示游戏终止时掷硬币的次数.
表示游戏终止时掷硬币的次数.
(1)求![]() 的取值范围;
的取值范围;
(2)求![]() 的数学期望E
的数学期望E![]() .
.
全国卷(Ⅰ)理
解答题
(20)(本大题满分12分)
9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为![]() ,若一个坑内至少
,若一个坑内至少
有1粒种子发芽,则这个坑不需要补种; 若一个坑内的种子都没发芽,则这个坑
需要补种![]() 假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,
假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,
写出ξ的分布列并求ξ的数学期望![]() (精确到
(精确到![]() )
)
全国卷(Ⅱ)理
解答题
(19)(本小题满分12分)
甲、乙两队进行一场排球比赛.根据以往经验,单局比赛甲队胜乙队的概率为0.6,
本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没
有影响.令![]() 为本场比赛的局数.求
为本场比赛的局数.求![]() 的概率分布和数学期望.(精确到0.0001)
的概率分布和数学期望.(精确到0.0001)
全国卷(Ⅲ)理
填空题(每小题4分)
15.设![]() 为平面上过点(0,1)的直线,
为平面上过点(0,1)的直线,![]() 的斜率等可能地取-2
的斜率等可能地取-2![]() ,-
,-![]() ,-
,-![]() ,0,
,0,![]() ,
,
![]() ,
2
,
2![]() ,
用ξ表示坐标原点到
,
用ξ表示坐标原点到![]() 的距离,则随机变量ξ的数学期望Eξ=
的距离,则随机变量ξ的数学期望Eξ=
![]()
解答题
17.(本小题满分12分)
甲.乙.丙三台机器是否需要照顾相互之间没有影响![]() 已知在某一个小时内,甲.乙
已知在某一个小时内,甲.乙
都需要照顾的概率是0.05,甲.丙都需要照顾的概率是0.05,乙.丙都需要照顾的
概率是0.125![]()
1)求甲.乙.丙三台机器在这一个小时内各自需要照顾的概率?
2)计算在这一个小时内至少有一台需要照顾的概率?
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。