解答题

18．（本小题满分14分）

某城市有甲、乙、丙3个旅游景点，一位客人游览这三个景点的概率分别

是0.4，0.5，0.6，且客人是否游览哪个景点互不影响，设ξ表示客人离开

该城市时游览的景点数与没有游览的景点数之差的绝对值.

（Ⅰ）求ξ的分布及数学期望；

（Ⅱ）记“函数f(x)＝x²－3ξx＋1在区间[2，＋∞上单调递增”为

事件A，求事件A的概率. 

解：

（I）分别记“客人游览甲景点”，“客人游览乙景点”，“客人游览丙景点”

 为事件A1，A2，A3. 由已知A1，A2，A3相互独立，P（A1）=0.4，

  P（A2）=0.5，P（A3）=0.6.

    客人游览的景点数的可能取值为0，1，2，3. 相应地，客人没有游览

    的景点数的可能取值为3，2，1，0，所以的可能取值为1，3.

       P（=3）=P（A1·A2·A3）+ P（）

      = P（A1）P（A2）P（A3）+P（）

      =2×0.4×0.5×0.6=0.24，

1    

3  

P

0.76

0.24

       P（=1）=1－0.24=0.76.

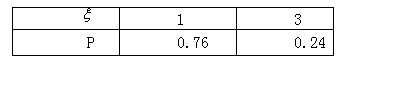
       所以的分布列为

       E=1×0.76+3×0.24=1.48.

（Ⅱ）解法一  因为

所以函数上单调递增，

要使上单调递增，当且仅当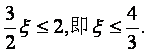

从而

解法二：的可能取值为1，3.

当=1时，函数上单调递增，

当=3时，函数上不单调递增.

所以