解答题

全国卷Ⅰ(文)

2004年

20．（本小题满分12分）

从10位同学（其中6女，4男）中随机选出3位参加测验.每位女同学能通过

测验的概率均为，每位男同学能通过测验的概率均为.试求：

（I）选出的3位同学中，至少有一位男同学的概率；

（II）10位同学中的女同学甲和男同学乙同时被选中且通过测验的概率.

 解答

2005年

（20）（本大题满分12分）

9粒种子分种在甲、乙、丙3个坑内，每坑3粒，每粒种子发芽的概率为，若一个

坑内至少有1粒种子发芽，则这个坑不需要补种；若一个坑内的种子都没发芽，

则这个坑需要补种

（Ⅰ）求甲坑不需要补种的概率；

（Ⅱ）求3个坑中恰有1个坑不需要补种的概率；

（Ⅲ）求有坑需要补种的概率

（精确到）

解答

2006年

(20) (本小题满分12分)

如图，l、l是互相垂直的异面直线，MN是它们的公垂线段.点A、B在上l，

C在l上,AM=MB=MN.

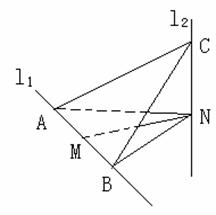
（Ⅰ）证明AC；

（Ⅱ）若，求NB与平面ABC所成角的余弦值.

解答

2007年

（20）（本小题满分12分）

设函数在及时取得极值．

（Ⅰ）求a、b的值；

（Ⅱ）若对于任意的，都有成立，求c的取值范围．

解答

全国卷Ⅱ(文)

2004年

20．（本小题满分12分）

   如图，直三棱柱ABC—A₁B₁C₁中，∠ACB=90°，AC=1，CB=，

侧棱AA₁=1，侧面AA₁B₁B的两条对角线交点为D，B₁C₁的中点为M.

（Ⅰ）求证CD⊥平面BDM；

（Ⅱ）求面B₁BD与面CBD所成二面角的大小.

           解答

2005年

（20）（本小题满分12分）

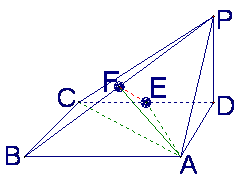     如图，四棱锥P-ABCD中，底面ABCD为矩形，PD垂直于底面ABCD，AD=PD，E、F分别

     为CD、PB的中点．

    （Ⅰ）求证：EF垂直于平面PAB；

    （Ⅱ）设AB=BC，求AC与平面AEF所成的角的大小．

解答

2006年

（20）（本小题１２分）

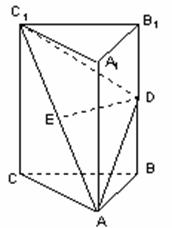
 如图，在直三棱柱中，、分别为、的中点。

（I）证明：ED为异面直线与的公垂线；

（II）设求二面角的大小

  解答

2007年

20．（本小题满分12分）

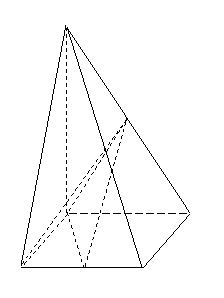
如图，在四棱锥中，

底面为正方形，侧棱底面

分别为的中点．

（1）证明平面；

（2）设，求二面角的大小．

解答

全国卷Ⅲ(文)

2004年

20．（本小题满分12分）某村计划建造一个室内面积为800的矩形蔬菜温室。

在温室内，沿左．右两侧与后侧内墙各保留1宽的通道，沿前侧内墙保留3宽

的空地。当矩形温室的边长各为多少时？蔬菜的种植面积最大。最大种植面积是多少？

解答

2005年

（20）(本小题满分12分)

在等差数列中，公差，是与的等差中项，已知数列,,,,

    ……,,……成等比数列，求数列的通项

解答

全国卷Ⅳ(文)

2004年

20．（本小题满分12分）

   某同学参加科普知识竞赛，需回答3个问题.竞赛规则规定：答对

第一、二、三问题分别得100分、100分、200分，答错得零分.假设这

名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6，且各题

答对与否相互之间没有影响.

（Ⅰ）求这名同学得300分的概率；

（Ⅱ）求这名同学至少得300分的概率.

解答

北京卷(文)

2004年

（18）（本小题满分14分）

    函数定义在［0，1］上，满足且，在每个区间

（1，2……）上，的图象都是平行于x轴的直线的一部分。

    （I）求及，的值，并归纳出的表达式

    （II）设直线，，x轴及的图象围成的矩形的面积

为（1，2……），求及的值

     解答

2005年

(18)(本小题共13分)

   甲、乙俩人各进行3次射击,甲每次击中目标的概率为,乙每次击中目标的概率为.

(Ⅰ)记甲恰好击中目标2次的概率;

(Ⅱ)求乙至少击中目标2次的概率;

(Ⅲ)求乙恰好比甲多击中目标2次的概率;

解答

2006年

(18)(本小题共13分)

    某公司招聘员工，指定三门考试课程，有两种考试方案．

    方案一：考试三门课程，至少有两门及格为考试通过：

    方案二：在三门课程中，随机选取两门，这两门都及格为考试通过．

    假设某应聘者对三门指定课程考试及格的概率分别是0．5，0．6，0．9，

且三门课程考试是否及格相互之间没有影响．求：

(Ⅰ)该应聘者用方案一考试通过的概率；

(Ⅱ)该应聘者用方案二考试通过的概率．

解答

2007年

18．（本小题共12分）

某条公共汽车线路沿线共有11个车站（包括起点站和终点站），在起点站开出的一辆

公共汽车上有6位乘客，假设每位乘客在起点站之外的各个车站下车是等可能的．求：

（I）这6位乘客在其不相同的车站下车的概率；

（II）这6位乘客中恰有3人在终点站下车的概率；

解答

天津卷(文)

2004年

20.（本小题满分12分）

设是一个公差为的等差数列，它的前10项和

且，，成等比数列。

（1）证明；（2）求公差的值和数列的通项公式。

解答

2005年

（20）（本小题满分12）

    某人在一山坡P处观看对面山项上的一座铁塔，如图所示，塔高BC=80（米），

    塔所在的山高OB=220（米），OA=200（米），

    图中所示的山坡可视为直线且点P在直线上，

    与水平地面的夹角为 ,tan=1/2试问此人

    距水平地面多高时，观看塔的视角∠BPC最大

   （不计此人的身高） 

解答

2006年

(20)(本小题满分12分)

    已知函数f(x)=4x³-3x²cosθ+，其中x∈R，θ为参数，且0≤θ≤.

    (Ⅰ)当cosθ=0时，判断函数f(x)是否有极值；

    (Ⅱ)要使函数f(x)的极小值大于零，求参数θ的取值范围；

    (Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数θ，函数f(x)在区间(2a-1，a)

内都是增函数，求实数a的取值范围.

 解答

2007年

（20）（本小题满分12分）

在数列中，，，．

（Ⅰ）证明数列是等比数列；

（Ⅱ）求数列的前项和；

（Ⅲ）证明不等式，对任意皆成立．

解答

上海卷(文)

2004年

20、(本题满分14分) 第1小题满分6分, 第2小题满分8分

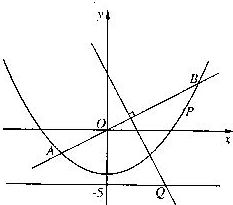如图, 直线y=x与抛物线y=x²－4交于A、B两点, 线段AB的垂直

平分线与直线y=－5交于Q点.

 (1) 求点Q的坐标；

(2) 当P为抛物线上位于线段AB下方

(含A、B) 的动点时, 求ΔOPQ面积的最大值.

解答 

2005年

20.（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分

假设某市2004年新建住房400万平方米，其中有250万平方米是中低价房预计

在今后的若干年内，该市每年新建住房面积平均比上一年增长8%，另外，每年新

建住房中，中低价房的面积均比上一年增加50万平方米那么，到那一年底，

（1）该市历年所建中低价房的累计面积（以2004年为累计的第一年）将首次不少

于4750万平方米？

（2）当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%？

解答

2006年

20(本题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分.

设数列{a_n}的前n项和为S_n，且对任意正整数n，a_n+S_n=4096.

(1)求数列{a_n}的通项公式：

(2)设数列{log₂a_n}的前n项和为T_n.对数列{T_n}，从第几项起T_n＜-509？

解答

2007年

19．（本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．

    已知函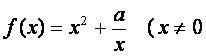数，常数．

    （1）当时，解不等式；

    （2）讨论函数的奇偶性，并说明理由．

解答

辽宁卷（文）

2004年

20．（本小题满分12分）

甲方是一农场，乙方是一工厂. 由于乙方生产须占用甲方的资源，因此

甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付

甲方的情况下，乙方的年利润x（元）与年产量t（吨）满足函数关系

.若乙方每生产一吨产品必须赔付甲方s元（以下称s为赔付价格），

   （1）将乙方的年利润w（元）表示为年产量t（吨）的函数，并求出乙方

获得最大利润的年产量；

   （2）甲方每年受乙方生产影响的经济损失金额（元），在乙方

按照获得最大利润的产量进行生产的前提下，甲方要在索赔中获得最大净收入，

应向乙方要求的赔付价格s是多少？

解答

2005年

    20．（本小题满分12分）

 某工厂生产甲、乙两种产品，每种产品都是经过第一和第二工序加工而成，

 两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级.对

 每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均为二等品.

   （Ⅰ）已知甲、乙两种产品每一道工序的加工结果为A级的概率如表一所示，

    分别求生产出的甲、乙产品为一等品的概率P甲、P乙；

   （Ⅱ）已知一件产品的利润如表二所示，用ξ、

         η分别表示一件甲、乙产品的利润，在

        （I）的条件下，求ξ、η的分布列及

Eξ、Eη；

   （Ⅲ）已知生产一件产品需用的工人数和资金额

         如表三所示.该工厂有工人40名，可用资

         品的数量，在（II）的条件下，x、y为何

         值时，最大？最大值是多少？

        （解答时须给出图示）                    

     解答

2006年（文）

20．（本小题满分12分）

已知等差数列的前项和为，．

（1）求的值；

（2）若与的等差中项为，满足，求数列的前项和．

 解答

2007年

20．（本小题满分12分）

已知数列，满足，，且（）

（I）令，求数列的通项公式；

（II）求数列的通项公式及前项和公式．

解答

江苏卷

2004年

20.设无穷等差数列{a_n}的前n项和为S_n.

(Ⅰ)若首项  EQ \F(3,2) ，公差，求满足的正整数k；

(Ⅱ)求所有的无穷等差数列{a_n}，使得对于一切正整数k都有成立.

解答

2005年

22.（本小题满分14分，第一小问满分4分，第二小问满分10分）

已知，函数

  ⑴当时，求使成立的的集合；

  ⑵求函数在区间上的最小值

解答

2006年

（20）（本小题满分16分，第一小问4分，第二小问满分6分，第三小问满分6分）

　　　设a为实数，设函数的最大值为g(a)。

　　　（Ⅰ）设t＝，求t的取值范围，并把f(x)表示为t的函数m(t)

（Ⅱ）求g(a)

（Ⅲ）试求满足的所有实数a

解答

2007年

20．（本题满分16分）

已知是等差数列，是公比为的等比数列，，，

记为数列的前项和．

（1）若（是大于的正整数），求证：；（4分）

（2）若（是某个正整数），求证：是整数，且数列中的每一项

都是数列中的项；（8分）

（3）是否存在这样的正数，使等比数列中有三项成等差数列？

若存在，写出一个的值，并加以说明；若不存在，请说明理由．（4分）

解答

浙江卷(文)

2004年

（20）（本题满分12分）

某地区有5个工厂，由于用电紧缺，规定每个工厂在一周内必须选择

某一天停电（选哪一天是等可能的）。假定工厂之间的选择互不影响。

    （Ⅰ）求5个工厂均选择星期日停电的概率；

 （Ⅱ）求至少有两个工厂选择同一天停电的概率。

解答

2005年

18．如图，在三棱锥P－ABC中，AB⊥BC，AB＝BC＝PA，点O、D分别是AC、

   PC的中点，OP⊥底面ABC．

   (Ⅰ)求证∥平面

   (Ⅱ) 求直线与平面PBC所成角的大小；

解答

2006年

(18)甲、乙两袋装有大小相同的红球和白球，甲袋装有2个红球，2个白球；

乙袋装有2个红球，n个白球．现从甲、乙两袋中各任取2个球．

    (Ⅰ)若n=3，求取到的4个球全是红球的概率；

    (Ⅱ)若取到的4个球中至少有2个红球的概率为，求n．

解答

2007年

21．（本题15分）如图，直线与椭圆交于两点，记的面积为．

（I）求在，的条件下，的最大值；

（II）当，时，求直线的方程．

解答

福建卷(文)

2004年

20．（本小题满分12分）

某企业2003年的纯利润为500万元，因设备老化等原因，企业的生产能

力将逐年下降.若不能进行技术改造，预测从今年起每年比上一年纯利

润减少20万元，今年初该企业一次性投入资金600万元进行技术改造，

预测在未扣除技术改造资金的情况下，第n年（今年为第一年）的利润

为500(1+)万元（n为正整数）.

（Ⅰ）设从今年起的前n年，若该企业不进行技术改造的累计纯利润为

A_n万元，进行技术改造后的累计纯利润为B_n万元（须扣除技术改造资金），

求A_n、B_n的表达式；

（Ⅱ）依上述预测，从今年起该企业至少经过多少年，进行技术改造后的

累计纯利润超过不进行技术改造的累计纯利润？

  解答

2005年

20．（本小题满分12分）

已知函数的图象过点P（0，2），且在点M（－1，f（－1））

处的切线方程为.

   （Ⅰ）求函数的解析式；

 （Ⅱ）求函数的单调区间.

解答

2006年

（20）（本小题满分12分）

       已知椭圆的左焦点为F，O为坐标原点。

       （I）求过点O、F，并且与椭圆的左准线相切的圆的方程；

       （II）设过点F的直线交椭圆于A、B两点，并且线段AB的

              中点在直线上，求直线AB的方程。

      解答

2007年

20．（本小题满分12分）

设函数．

（Ⅰ）求的最小值；

（Ⅱ）若对恒成立，求实数的取值范围．

解答

湖北卷(文)

2004年

20．（本小题满分12分）

直线的右支交于不同的两点A、B.

（Ⅰ）求实数k的取值范围；

（Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？

若存在，求出k的值；若不存在，说明理由.

　解答

2005年

20．（本小题满分12分）

    如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的，

    其中AB=4，BC=2，CC1=3，BE=1

   （Ⅰ）求BF的长；

   （Ⅱ）求点C到平面AEC1F的距离

    解答

    2006年

19．（本小题满分12分）

设函数f（x）=x³-ax²+bx+c在x=1处取得极值-2，试用c表示a和b，并求f（x）

的单调区间。

解答

2007年

19．（本小题满分12分）

设二次函数，方程的两根和满足．

（I）求实数的取值范围；

（II）试比较与的大小．并说明理由．

 解答

湖南卷(文)

2004年

20．（本小题满分12分）

    已知数列{a_n}是首项为a且公比q不等于1的等比数列，S_n是其前n项的和，

a₁,2a₇,3a₄ 成等差数列.

（I）证明  12S₃,S₆,S₁₂-S₆成等比数列；

（II）求和T_n=a₁+2a₄+3a₇+…+na_3n-2.

解答

2005年

19．（本小题满分14分）

     设，点P（，0）是函数的图象的一个

     公共点，两函数的图象在点P处有相同的切线

  （Ⅰ）用表示a，b，c；

  （Ⅱ）若函数在（－1，3）上单调递减，求的取值范围

解答

2006年

19．(本小题满分14分)

    已知函数f(x)=ax³-3x²+1-.

    (Ⅰ)讨论函数f(x)的单调性；

    (Ⅱ)若曲线y=f(x)上两点A、B处的切线都与y轴垂直，且线段AB与x轴有公共点，

求实数a的取值范围.

解答

2007年

19．（本小题满分13分）

已知双曲线的右焦点为，过点的动直线与双曲线相交于两点，

点的坐标是．

（I）证明，为常数；

（II）若动点满足（其中为坐标原点），求点的轨迹方程．

解答

广东卷（文）

2004年

20 (12分)某中心接到其正东、正西、正北方向三个观测点的报告：正西、

正北两个观测点同时听到了一声巨响，正东观测点听到的时间比其他两观

测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生

的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上)

 解答

2005年

18．（本小题满分12分）

箱中装有大小相同的黄、白两种颜色的乒乓球，黄、白乒乓球的数量比为s:t.

现从箱中每次任意取出一个球，若取出的是黄球则结束，若取出的是白球，则

将其放回箱中，并继续从箱中任意取出一个球，但取球的次数最多不超过n次，

以ξ表示取球结束时已取到白球的次数.

   （Ⅰ）求ξ的分布列；

   （Ⅱ）求ξ的数学期望.

解答

2006年

18．（本小题满分14分）

    设函数f(x)=-x³+3x+2分别在x₁、x₂处取得极小值、极大值。xoy平面

上点A、B的坐标分别为（x₁，f(x₁)）、（x₂，f(x₂)）。该平面上动点P满

足，点Q是点P关于直线y=2(x-4)的对称点，求：

（Ⅰ）点A、B的坐标：

（Ⅱ）动点Q的轨迹方程。

解答

2007年

19．（本小题满分14分）

在平面直角坐标系中，已知圆心在第二象限，半径为的圆与直线

相切于坐标原点，椭圆与圆的一个交点到椭圆两焦点的距离之和为．

（1）求圆的方程；

（2）试探究圆上是否存在异于原点的点，使到椭圆右焦点的距离等于

线段的长．若存在，请求出点的坐标；若不存在，请说明理由．

解答

重庆卷(文)

2004年

20．（本小题满分12分）

     某工厂生产某种产品，已知该产品的月生产量（吨）与每吨产品的价格

（元/吨）之间的关系式为：,且生产x吨的成本为（元）。

问该产每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）

解答

2005年

20．（本小题满分13分）

  如图，在四棱锥P—ABCD中，底面ABCD为矩形，PD⊥底面ABCD，E是AB上一点，

  PE⊥EC. 已知求

   （Ⅰ）异面直线PD与EC的距离；

   （Ⅱ）二面角E—PC—D的大小.

解答

2006年

(20)（本小题满分12分）

如图，在正四棱柱ABCD-A₁B₁C₁D₁中：AB=1，BB₁=+1，E为BB₁上

使B₁E=1的点，平面AEC₁交DD₁于F，交A₁D₁的延长线于G.求：

（Ⅰ）异面直线AD与C₁G所成的角的大小；

（Ⅱ）二面角A-C₁G-A₁的正切值.

        解答

2007年

20．（本小题满分12分）

用长为18m的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为，

问该长方体的长、宽、高各为多少时，其体积最大？最大体积是多少？

解答

山东卷(文)

2005年

 (20) （本小题满分12分）

如图，已知长方体，，直线与平面

所成的角为，垂直于为的中点．

（Ⅰ）求异面直线与所成的角；

（Ⅱ）求平面与平面所成二面角（锐角）的大小；

（Ⅲ）求点到平面的距离 

解答

2006年

(20) （本小题满分12分）

如图，已知四棱锥P-ABCD的底面ABCD为等腰梯形，AB∥CD,AC⊥BD,AC与BD

相交于点O，且顶点P在底面上的射影恰为O点，又BO=2,PO=,PB⊥PD.

(Ⅰ)求异面直线PD与BC所成角的余弦值；

(Ⅱ)求二面角P-AB-C的大小；

(Ⅲ)设点M在棱PC上，且为何值时，PC⊥平面BMD.

解答

2007年

20．（本小题满分12分）

    如图，在直四棱柱中，

已知，．

（1）求证：；

（2）设是上一点，试确定的位置，

使平面

，并说明理由．

解答

江西卷(文)

2005年

20．（本小题满分12分）

如图，在长方体ABCD—A1B1C1D1，中，AD=AA1=1，AB=2，点E在棱AB上移动.

   （1）证明：D1E⊥A1D；

   （2）当E为AB的中点时，求点E到面ACD1的距离；

   （3）AE等于何值时，二面角D1—EC—D的大小为.

      解答

2006年

20．(本小题满分12分)

如图，已知三棱锥O-ABC的侧棱OA、OB、OC两两垂直，且OA=1，OB=OC=2，

E是OC的中点．

    (1)求O点到面ABC的距离；

    (2)求异面直线BE与AC所成的角；

    (3)求二面角E-AB-C的大小．

解答

2007年

20．（本小题满分12分）

右图是一个直三棱柱（以为底面）被一平面所截得到的几何体，截面为．

已知，，，，．

（1）设点是的中点，证明：平面；

（2）求与平面所成的角的大小；

（3）求此几何体的体积．

解答

陕西卷(文)

2006年

20．（本小题满分12分）

已知正项数列，其前n项和S_n满足10S_n=＋5a_n＋6，

且a₁，a₃，a₁₅成等比数列，求数列的通项a_n.

解答

2007年

20．（本小题满分12分）

已知实数列是等比数列，其中，且，成等差数列．

（Ⅰ）求数列的通项公式；

（Ⅱ）数列的前项和记为，证明：．

解答

四川卷(文)

2006年

（20）（本大题满分12分）

如图，在长方体中，分别是的中点，

分别是的中点，

（Ⅰ）求证：面；

（Ⅱ）求二面角的大小。

解答

2007年

（20）(本小题满分12分)

设函数f（x）=ax3+bx+c（a≠0）为奇函数，其图象在点（1,f（1））处的切线

与直线x－6y－7=0垂直，导函数f＇（x）的最小值为－12.

（Ⅰ）求a，b，c的值；

（Ⅱ）求函数f（x）的单调递增区间，并求函数f（x）在〔－1,3〕上的最大值和最小值.

解答

安徽卷(文)

2006年

（20）（本大题满分12分）设函数，已知

是奇函数。

（Ⅰ）求、的值。

（Ⅱ）求的单调区间与极值。

     解答

2007年

19．（本小题满分13分）

在医学生物试验中，经常以果蝇作为试验对象．一个关有6只果蝇的笼子里，

不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把

笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔．

（I）求笼内恰好剩下1只果蝇的概率；

（II）求笼内至少剩下5只果蝇的概率．

解答

海南宁夏卷(文)

2007年

20．（本小题满分12分）

设有关于的一元二次方程．

（Ⅰ）若是从四个数中任取的一个数，是从三个数中任取的一个数，

求上述方程有实根的概率．

（Ⅱ）若是从区间任取的一个数，是从区间任取的一个数，

求上述方程有实根的概率．

解答