解答题
全国卷Ⅰ(理)
(21)(本小题满分12分)
已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过
.过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,
两点,
过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]() ,垂足为
,垂足为![]() .
.
(Ⅰ)设![]() 点的坐标为
点的坐标为![]() ,证明:
,证明: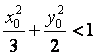 ;
;
(Ⅱ)求四边形![]() 的面积的最小值.
的面积的最小值.
全国卷Ⅱ(理)
21.(本小题满分12分)
设数列![]() 的首项
的首项![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,证明
,证明![]() ,其中
,其中![]() 为正整数.
为正整数.
北京卷(理)
19.(本小题共13分)
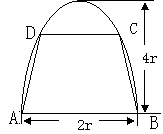 如图,有一块半椭圆形钢板,其半轴长为
如图,有一块半椭圆形钢板,其半轴长为![]() ,短半轴长为
,短半轴长为![]() ,计划将此钢板切割成
,计划将此钢板切割成
等腰梯形的形状,下底![]() 是半椭圆的短轴,上底
是半椭圆的短轴,上底![]() 的端点在椭圆上,
的端点在椭圆上,
记![]() ,梯形面积为
,梯形面积为![]() .
.
(I)求面积![]() 以
以![]() 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;
(II)求面积![]() 的最大值.
的最大值.
天津卷(理)
21.(本小题满分14分)
在数列![]() 中,
中,![]() ,其中
,其中![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)证明存在![]() ,使得
,使得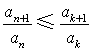 对任意
对任意![]() 均成立.
均成立.
上海卷(理)
20.(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分6分,
第3小题满分9分.
如果有穷数列![]() (
(![]() 为正整数)满足条件
为正整数)满足条件![]() ,
,![]() ,
,
…,![]() ,即
,即![]() (
(![]() ),我们称其为“对称数列”.例如,
),我们称其为“对称数列”.例如,
由组合数组成的数列![]() 就是“对称数列”.
就是“对称数列”.
(1)设![]() 是项数为7的“对称数列”,其中
是项数为7的“对称数列”,其中![]() 是等差数列,且
是等差数列,且![]() ,
,
![]() .依次写出
.依次写出![]() 的每一项;
的每一项;
(2)设![]() 是项数为
是项数为![]() (正整数
(正整数![]() )的“对称数列”,其中
)的“对称数列”,其中![]() 是
是
首项为![]() ,公差为
,公差为![]() 的等差数列.记
的等差数列.记![]() 各项的和为
各项的和为![]() .当
.当![]() 为何值时,
为何值时,
![]() 取得最大值?并求出
取得最大值?并求出![]() 的最大值;
的最大值;
(3)对于确定的正整数![]() ,写出所有项数不超过
,写出所有项数不超过![]() 的“对称数列”,
的“对称数列”,
使得![]() 依次是该数列中连续的项;当
依次是该数列中连续的项;当![]()
![]() 时,求其中一个
时,求其中一个
“对称数列”前![]() 项的和
项的和![]() .
.
辽宁卷(理)
21.(本小题满分12分)
已知数列![]() ,
,![]() 与函数
与函数![]() ,
,![]() ,
,![]() 满足条件:
满足条件:
![]() ,
,![]() .
.
(I)若![]() ,
,![]() ,
,![]() ,
,![]() 存在,求
存在,求![]() 的取值范围;
的取值范围;
(II)若函数![]() 为
为![]() 上的增函数,
上的增函数,![]() ,
,![]() ,
,![]() ,证明对任意
,证明对任意![]() ,
,
![]() (用
(用![]() 表示).
表示).
江苏卷
21.(本题满分16分)
已知![]() 是不全为零的实数,函数
是不全为零的实数,函数![]() ,
,![]() .
.
方程![]() 有实数根,且
有实数根,且![]() 的实数根都是
的实数根都是![]() 的根;反之,
的根;反之,
![]() 的实数根都是
的实数根都是![]() 的根.
的根.
(1)求![]() 的值;(3分)
的值;(3分)
(2)若![]() ,求
,求![]() 的取值范围;(6分)
的取值范围;(6分)
(3)若![]() ,
,![]() ,求
,求![]() 的取值范围.(7分)
的取值范围.(7分)
浙江卷(理)
(22)(本题15分)设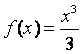 ,对任意实数
,对任意实数![]() ,记
,记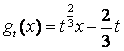 .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)求证:(ⅰ)当![]() 时,
时,![]()
![]() 对任意正实数
对任意正实数![]() 成立;
成立;
(ⅱ)有且仅有一个正实数![]() ,使得
,使得![]() 对任意正实数
对任意正实数![]() 成立.
成立.
福建卷(理)
21.(本小题满分12分)
等差数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(Ⅰ)求数列![]() 的通项
的通项![]() 与前
与前![]() 项和
项和![]() ;
;
(Ⅱ)设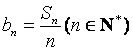 ,求证:数列
,求证:数列![]() 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
湖北卷(理)
20.(本小题满分13分)
已知定义在正实数集上的函数![]() ,
,![]() ,其中
,其中![]() .
.
设两曲线![]() ,
,![]() 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(I)用![]() 表示
表示![]() ,并求
,并求![]() 的最大值;
的最大值;
(II)求证:![]() (
(![]() ).
).
湖南卷(理)
20.(本小题满分12分)
已知双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的动直线与双曲线
的动直线与双曲线
相交于![]() 两点.
两点.
(I)若动点![]() 满足
满足![]() (其中
(其中![]() 为坐标原点),求点
为坐标原点),求点![]() 的轨迹方程;
的轨迹方程;
(II)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使
,使![]() ·
·![]() 为常数?若存在,求出点
为常数?若存在,求出点![]() 的坐标;
的坐标;
若不存在,请说明理由.
广东卷(理)
20.(本小题满分14分)
已知![]() 是实数,函数
是实数,函数![]() ,如果函数
,如果函数![]() 在区间
在区间![]() 上有零点,
上有零点,
求![]() 的取值范围.
的取值范围.
重庆卷(理)
21.(本小题满分12分,其中(Ⅰ)小问5分,(Ⅱ)小问7分.)
已知各项均为正数的数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 满足
满足![]() ,并记
,并记![]() 为
为![]() 的前
的前![]() 项和,求证:
项和,求证:
![]() .
.
山东卷(理)
(21)(本小题满分12分)
已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,椭圆
轴上,椭圆![]() 上的点到焦点距离的
上的点到焦点距离的
最大值为![]() ,最小值为
,最小值为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点(
两点(![]() 不是左右顶点),
不是左右顶点),
且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的右顶点,求证:直线
的右顶点,求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
江西卷(理)
21.(本小题满分12分)
 设动点
设动点![]() 到点
到点![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,
,![]() ,且存在常数
,且存在常数![]() ,
,
使得![]() .
.
(1)证明:动点![]() 的轨迹
的轨迹![]() 为双曲线,并求出
为双曲线,并求出![]() 的方程;
的方程;
(2)过点![]() 作直线双曲线
作直线双曲线![]() 的右支于
的右支于![]() 两点,
两点,
试确定![]() 的范围,使
的范围,使![]() ,其中点
,其中点![]() 为坐标原点.
为坐标原点.
陕西卷(理)
21.(本小题满分14分)
已知椭圆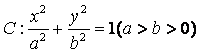 的离心率为
的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
求![]() 面积的最大值.
面积的最大值.
四川卷(理)
(21)(本小题满分12分)
已知函数![]() ,设曲线
,设曲线![]() 在点
在点![]() 处的切线与X轴的交点
处的切线与X轴的交点![]() ,
,
其中x1为正实数。
(Ⅰ)用xn表示xn+1;
(Ⅱ)求证:对一切正整数n,![]() 的充要条件是
的充要条件是![]() ;
;
(Ⅲ)若x1=4,记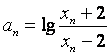 ,证明数列{an}成等比数列,并求数列{an}的通项公式。
,证明数列{an}成等比数列,并求数列{an}的通项公式。
安徽卷(理)
20.(本小题满分13分)
在医学生物学试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,
不慎混入了两只苍蝇(此时笼内共有8只蝇子,6只果蝇和2只苍蝇),只好把
笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭
小孔.以![]() 表示笼内还剩下的果蝇的只数.
表示笼内还剩下的果蝇的只数.
(Ⅰ)写出![]() 的分布列(不要求写出计算过程);
的分布列(不要求写出计算过程);
(Ⅱ)求数学期望![]() ;
;
(Ⅲ)求概率![]() .
.
海南宁夏卷(理)
21.(本小题满分12分)
设函数![]()
(I)若当![]() 时,
时,![]() 取得极值,求
取得极值,求![]() 的值,并讨论
的值,并讨论![]() 的单调性;
的单调性;
(II)若![]() 存在极值,求
存在极值,求![]() 的取值范围,并证明所有极值之和大于
的取值范围,并证明所有极值之和大于![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。