三、解答题

21．（本题满分16分）

已知是不全为零的实数，函数，．

方程有实数根，且的实数根都是的根；反之，

的实数根都是的根．

（1）求的值；（3分）

（2）若，求的取值范围；（6分）

（3）若，，求的取值范围．（7分）

本小题主要考查函数、方程、不等式的基本知识，考查综合运用分类讨论、

等价转化等思想方法分析问题及推理论证的能力．满分16分．

解：（1）设为方程的一个根，即，则由题设得．于是，

，即．

所以，．

（2）由题意及（1）知，．

由得是不全为零的实数，且，

则．

方程就是．①

方程就是．②

（ⅰ）当时，，方程①、②的根都为，符合题意．

（ⅱ）当，时，方程①、②的根都为，符合题意．

（ⅲ）当，时，方程①的根为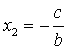，，它们也都是方程②的根，

但它们不是方程的实数根．

由题意，方程无实数根，此方程根的判别式，

得．

综上所述，所求的取值范围为．

（3）由，得，，

．③

由可以推得，知方程的根一定是方程的根．

当时，符合题意．

当时，，方程的根不是方程　④

的根，因此，根据题意，方程④应无实数根．

那么当，即时，，符合题意．

当，即或时，由方程④得，

即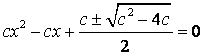，⑤

则方程⑤应无实数根，所以有且．

当时，只需，解得，矛盾，舍去．

当时，只需，解得．

因此，．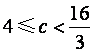

综上所述，所求的取值范围为．