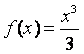 ,对任意实数
,对任意实数 .
.三、解答题
(22)(本题15分)设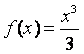 ,对任意实数
,对任意实数![]() ,记
,记 .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)求证:(ⅰ)当![]() 时,
时,![]()
![]() 对任意正实数
对任意正实数![]() 成立;
成立;
(ⅱ)有且仅有一个正实数![]() ,使得
,使得![]() 对任意正实数
对任意正实数![]() 成立.
成立.
本题主要考查函数的基本性质,导数的应用及不等式的证明等基础知识,
以及综合运用所学知识分析和解决问题的能力.满分15分.
(I)解: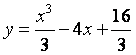 .
.
由![]() ,得
,得
![]() .
.
因为当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
故所求函数的单调递增区间是![]() ,
,![]() ,
,
单调递减区间是![]() .
.
(II)证明:(i)方法一:
令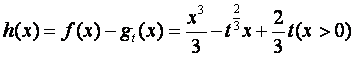 ,则
,则
![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 内的最小值是
内的最小值是![]() .
.
故当![]() 时,
时,![]() 对任意正实数
对任意正实数![]() 成立.
成立.
方法二:
对任意固定的![]() ,令
,令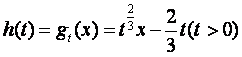 ,则
,则
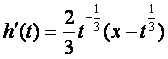 ,
,
由![]() ,得
,得![]() .
.
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 取得最大值
取得最大值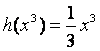 .
.
因此当![]() 时,
时,![]() 对任意正实数
对任意正实数![]() 成立.
成立.
(ii)方法一:
![]() .
.
由(i)得,![]() 对任意正实数
对任意正实数![]() 成立.
成立.
即存在正实数![]() ,使得
,使得![]() 对任意正实数
对任意正实数![]() 成立.
成立.
下面证明![]() 的唯一性:
的唯一性:
当![]() ,
,![]() ,
,![]() 时,
时,
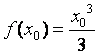 ,
, ,
,
由(i)得,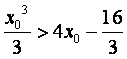 ,
,
再取![]() ,得
,得 ,
,
所以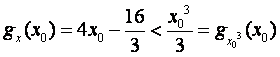 ,
,
即![]() 时,不满足
时,不满足![]() 对任意
对任意![]() 都成立.
都成立.
故有且仅有一个正实数![]() ,
,
使得![]() 对任意正实数
对任意正实数![]() 成立.
成立.
方法二:对任意![]() ,
,![]() ,
,
因为![]() 关于
关于![]() 的最大值是
的最大值是![]() ,所以要使
,所以要使![]() 对任意正实数成立的充分
对任意正实数成立的充分
必要条件是:
![]() ,
,
即![]() ,
①
,
①
又因为![]() ,不等式①成立的充分必要条件是
,不等式①成立的充分必要条件是![]() ,
,
所以有且仅有一个正实数![]() ,
,
使得![]() 对任意正实数
对任意正实数![]() 成立.
成立.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。