三、解答题
21.(本小题满分14分)
在数列![]() 中,
中,![]() ,其中
,其中![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)证明存在![]() ,使得
,使得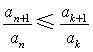 对任意
对任意![]() 均成立.
均成立.
本小题以数列的递推关系式为载体,主要考查等比数列的前![]() 项和公式、数列求和、
项和公式、数列求和、
不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识
分析问题和解决问题的能力.满分14分.
(Ⅰ)解法一:![]() ,
,
![]() ,
,
![]() .
.
由此可猜想出数列![]() 的通项公式为
的通项公式为![]() .
.
以下用数学归纳法证明.
(1)当![]() 时,
时,![]() ,等式成立.
,等式成立.
(2)假设当![]() 时等式成立,即
时等式成立,即![]() ,
,
那么![]()
![]()
![]() .
.
这就是说,当![]() 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式![]()
对任何![]() 都成立.
都成立.
解法二:由![]() ,
,![]() ,
,
可得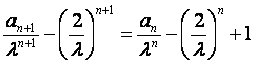 ,
,
所以 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故 ,
,
所以数列![]() 的通项公式为
的通项公式为![]() .
.
(Ⅱ)解:设![]() , ①
, ①
![]() ②
②
当![]() 时,①式减去②式,
时,①式减去②式,
得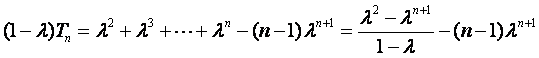 ,
,
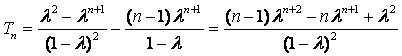 .
.
这时数列![]() 的前
的前![]() 项和
项和 .
.
当![]() 时,
时, .这时数列
.这时数列![]() 的前
的前![]() 项和
项和![]() .
.
(Ⅲ)证明:通过分析,推测数列![]() 的第一项
的第一项![]() 最大,下面证明:
最大,下面证明:
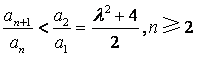 . ③
. ③
由![]() 知
知![]() ,要使③式成立,只要
,要使③式成立,只要![]() ,
,
因为![]()
![]()
![]() .
.
所以③式成立.
因此,存在![]() ,使得
,使得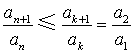 对任意
对任意![]() 均成立.
均成立.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。