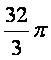，那么正方体的棱长等于(
)福建（文）
一、选择题(每题5分)
（7）已知正方体外接球的体积是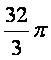，那么正方体的棱长等于(
)
（A）
（B）
（C）
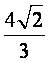（D）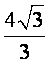
（10）对于平面
和共面的直线
、
下列命题中真命题是(
)
（A）若
则
（B）若
则
（C）若
则
（D）若
、
与
所成的角相等，则
三、解答题
（19）（本小题满分12分）
如图，四面体ABCD中，O、E分别是BD、BC的中点，
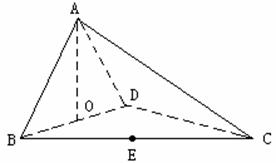
（I）求证：
平面BCD；
（II）求异面直线AB与CD所成角的大小；
（III）求点E到平面ACD的距离。
浙江（文）
一、选择题（每小题5分）
(8)如图，正三棱柱ABC-A1B1C1的各棱长都为2，E、F分别是AB、A1C1
的中点，则EF的长是（ ）
(A)2 (B)
(C)
(D)
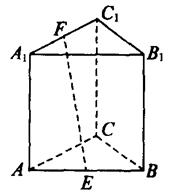
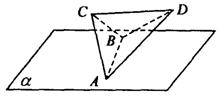
(14)如图，正四面体ABCD的棱长为1，平面α过棱AB，且CD∥α，则正四面体上
的所有点在平面α内的射影构成的图形面积是___________．
三、解答题
(17)如图，在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD=90°，
PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点．
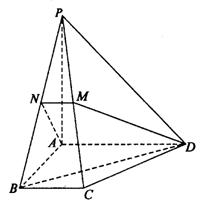
(Ⅰ)求证：PB⊥DM；
(Ⅱ)求BD与平面ADMN所成的角．
天津（文）
一、选择题（每小题5分）
（7）若l为一条直线，α、β、γ为三个互不重合的平面，给出下面三个命题：
①α⊥γ，β⊥γ
α⊥β；②α⊥γ,β∥γα⊥β；③l∥α，α⊥β
l⊥β.
其中正确的命题有（）
（A）0个 （B）1个 （C）2个 （D）3个
二、填空题（每小题4分）
（13）如图，在正三棱柱ABC-A1B1C1中，AB=1.若二面角C-AB-C1的
大小为60°，则点C1到直线AB的距离为__________.
三、解答题
(19)(本小题满分12分)
如图，在五面体ABCDEF中，点O是矩形ABCD的对角线的交点，
面CDE是等边三角形，棱EF
BC.
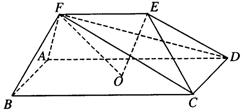
(Ⅰ)证明FO∥平面CDE；
(Ⅱ)设BC=
CD，证明EO⊥平面CDF
江苏
一、选择题（每小题5分）
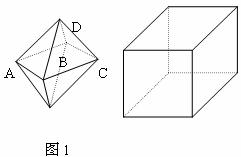
（9）两相同的正四棱锥组成如图1所示的几何体，可放棱长为1的正方体内，
使正四棱锥的底面ABCD与正方体的某一个平面平行，且各顶点均在正方体
的面上，则这样的几何体体积的可能值有()
（A）1个 （B）2个
（C）3个 （D）无穷多个
三、解答题
（18）（本小题满分14分）
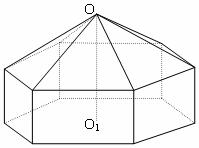
请您设计一个帐篷。它下部的形状是高为1m的正六棱柱，上部的形状是
侧棱长为3m的正六棱锥（如右图所示）。试问当帐篷的顶点O到底面中
心
的距离为多少时，帐篷的体积最大？
辽宁（文）
二、填空题(每题4分)
15．如图，半径为2的半球内有一内接正六棱锥
，则此正六
棱锥的侧面积是________．
三、解答题
19．（本小题满分12分）
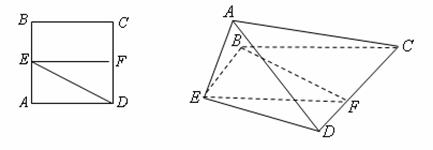
已知正方形
，
分别是边
的中点，将
沿
折起，
如图所示，记二面角
的大小为
（
）．
（1）证明
平面
；
（2）若
为正三角形，试判断点
在平面
内的射影
是否在直线
上，证明你的结论，并求角
的余弦值.
重庆（文）
一、选择题（每小题5分）
（4）若P是平面α外一点，则下列命题正确的是()
（A）过P只能作一条直线与平面α相交
（B）过P可作无数条直线与平面α垂直
（C）过P只能作一条直线与平面α平行
（D）过P可作无数条直线与平面α平行
三、解答题
(20)（本小题满分12分）
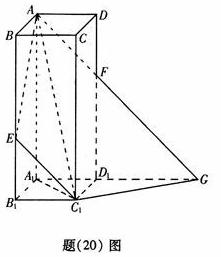
如图，在正四棱柱ABCD-A1B1C1D1中：AB=1，BB1=
+1，E为BB1上
使B1E=1的点，平面AEC1交DD1于F，交A1D1的延长线于G.求：
（Ⅰ）异面直线AD与C1G所成的角的大小；
（Ⅱ）二面角A-C1G-A1的正切值.
湖南（文）
一、选择题(每题5分)
4．过半径为2的球O表面上一点A作球O的截面，若OA与该截面所成的角是60°，
则该截面的面积是( )
A．π
B．2π
C．3π
D．2
π
二、填空题(每题4分)
14．过三棱柱ABC-A1B1C1任意两条棱的中点作直线，其中与平面ABB1A1平行的
直线共有 条．
三、解答题
18．(本小题满分14分)
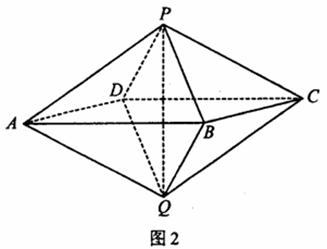
如图2，已知两个正四棱锥P-ABCD与Q-ABCD的高都为2，AB=4．
(Ⅰ)证明PQ⊥平面ABCD；
(Ⅱ)求异面直线AQ与PB所成的角；
(Ⅲ)求点P到平面QAD的距离．
湖北（文）
一、 选择题(每题5分)
6．关于直线m、n与平面α、β，有下列四个命题：
①若m∥α，n∥β且α∥β，则m∥n；
②若m⊥α，n⊥β且α⊥β，则m⊥n；
③若m⊥α，n∥β且α∥β，则m⊥n；
④若m∥α，n⊥β且α⊥β，则m∥n。
其中真命题的序号是( )
A．①、② B.③、④ C.①、④ D.②、③
二、填空题(每题5分)
15．半径为r的圆的面积S（r）=πr2，周长C（r）=2πr，若将r看作
（0，+∞）上的变量，
则（πr2）’=2πr ①
①式可用语言叙述为：圆的面积函数的导数等于圆的周长函数。
对于半径为R的球，若将R看作（0，+
）上的变量，请你写出类似于①的式子：
_______________________________________②
②式可用语言叙述为________________________________________。
三、解答题
18．（本小题满分12分）
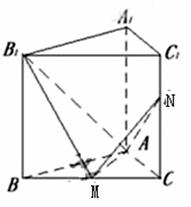
如图，已知正三棱柱ABC—A1B1C1的侧棱长和底面边长为1，M是底面BC边上的中点，
N是侧棱CC1上的点，且CN=2C1N。
（Ⅰ）求二面角B1—AM—N的平面角的余弦值；
（Ⅱ）求点B1到平面AMN的距离。
广东
一、选择题(每题5分)
12．若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为____。
三、解答题
17．（本小题满分14分）
如图所示，AF、DE分别是⊙
、⊙1的直径。AD与两圆所在的平面均
垂直，AD=8，BC是⊙的直径，AB=AC=6，OE//AD。
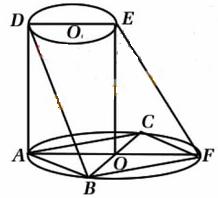
（Ⅰ）求二面角B-AD-F的大小；
（Ⅱ）求直线BD与EF所成的角。
北京（文）
一、选择提(每题5分)
(7)设A，B，C，D是空间四个不同的点．在下列命题中，不正确的是( )
(A)若AC与BD共面，则AD与BC共面
(B)若AC与BD是异面直线，则AD与BC是异面直线
(C)若AB=AC，DB=DC，则AD=BC
(D)若AB=AC，DB=DC，则AD⊥BC
二、填空题(每题4分)
(9)若三点A(2，2)，B(a，0)，C(0，4)共线，则a的值等于_______.
三、解答题
(17)(本小题共14分)
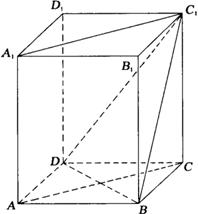
如图，ABCD-A1B1C1D1是正四棱柱.
(Ⅰ)求证：BD⊥平面ACC1A1；
(Ⅱ)若二面角C1-BD-C的大小为60°，求异面直线BC1与AC所成角的大小.
上海（文）
二、选择题（每小题4分）
15．若空间中有两条直线，则“这两条直线为异面直线”是“这两条直线
没有公共点”的（ ）
（A）充分非必要条件, (B)必要非充分条件，
（C）充分必要条件， （D）既非充分又非必要条件.
16.如果一条直线与一个平面垂直，那么，称此直钱与平面构成一个“正交
线面对”，在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面
构成的“正交线面对”的个数是（ ）
（A）48. (B)18. (C)24. (D)36.
三、解答题
19.（本题满分14分）本题共有2个小题，第1小题满分5分. 第2小题满分9分.
在直三棱柱ABC-A1B1C1中，∠ABC=90°.AB=BC=1，
（1）求异面直线B1C1与AC所成角的大小；
（2）若直线A1C与平面ABC所成角为45°.求三棱柱A1-ABC的结果.
山东（文）
一、选择题（每小题5分）
（8）正方体的内切球与其外接球的体积之比为（）
(A)1∶
(B)1∶3 (C)1∶3
(D)1∶9
二、填空题（每小题4分）
（16）如图，在正三棱柱ABC-
中，所有棱长均为1，
则点B
到平面ABC
的距离为 .
三、解答题
(20) （本小题满分12分）
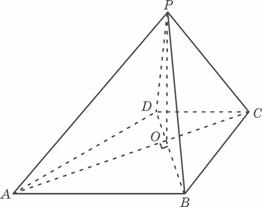如图，已知四棱锥P-ABCD的底面ABCD为等腰梯形，AB∥CD,AC⊥BD,AC与BD
相交于点O，且顶点P在底面上的射影恰为O点，又BO=2,PO=
,PB⊥PD.
(Ⅰ)求异面直线PD与BC所成角的余弦值；
(Ⅱ)求二面角P-AB-C的大小；
(Ⅲ)设点M在棱PC上，且
为何值时，PC⊥平面BMD.
江西（文）
一、选择题(每题5分)
9．如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰．
以下4个命题中，假命题是( )
A.等腰四棱锥的腰与底面所成的角都相等
B.等腰四棱锥的侧面与底面所成的二面角都相等或互补
C.等腰四棱锥的底面四边形必存在外接圆
D．等腰四棱锥的各顶点必在同一球面上
二、填空题(每题4分)
15．如图，已知正三棱柱ABC—A1B1C1的底面边长为1，高为8，一质点自A点出发，
沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为____________.
三、解答题
20．(本小题满分12分)
如图，已知三棱锥O-ABC的侧棱OA、OB、OC两两垂直，且OA=1，OB=OC=2，
E是OC的中点．
(1)求O点到面ABC的距离；
(2)求异面直线BE与AC所成的角；
(3)求二面角E-AB-C的大小．
陕西（文）
一、选择题（每小题5分）
11．已知平面α外不共线的三点A，B，C到α的距离相等，则正确的结论是（）
A．平面ABC必不垂直于α B．平面ABC必平行于α
C．平面ABC必与α相交 D．存在△ABC的一条中位线平行于α或在α内
二、填空题（每小题4分）
16．水平桌面
上放有4个半径均为2R的球，且相邻的球都相切（球心的
连线构成正方形）。在这4个球的上面放一个半径为R的小球，它和下面的
4个球恰好相切，则小球的球心到水平桌面
的距离是＿＿＿＿。
三、解答题
（１９）（本小题满分１２分）
如图，
点A在直线
上的射影为
点B在
上的射影为
已知
求：
（I）直线AB分别与平面
所成角的大小；
（II）二面角
的大小。
(第19题图)
安徽（文）
一、 选择提(每题5分)
（6）表面积为
的正八面体的各个顶点都在同一个球面上，则此球的体积为(
)
A．
B．
C．
D．
解答
二、填空题(每题4分)
（16）平行四边形的一个顶点A在平面
内，其余顶点在
的同侧，已知其中有两个顶点
到
的距离分
别为1和2 ，那么剩下的一个顶点到平面
的距离可能是：
①1； ②2； = 3 \* GB3 ③3； ④4；
以上结论正确的为______________。（写出所有正确结论的编号）
三、解答题
（19）（本大题满分12分）如图，P是边长为1的正六边形ABCDEF所在平面外一点，
，P在平面ABC内的射影为BF的中点O。
（Ⅰ）证明
⊥
；
（Ⅱ）求面
与面
所成二面角的大小。
四川（文）
一、选择题（每小题5分）
(7)
已知二面角
的大小为
，
为异面直线，且
，
则
所成的角为（）
（A）
（B）
（C）
（D）
(9)
如图，正四棱锥
底面的四个顶点
在球
的同一个大圆上，
点
在球面上，如果
，则球
的表面积是（）
（A）
（B）
（C）
（D）
二、填空题（每小题4分）
（16）
是空间两条不同直线，
是两个不同平面，下面有四个命题：
①
②
③
④
其中真命题的编号是________________;（写出所有真命题的编号）
三、解答题
（20）（本大题满分12分）
如图，在长方体
中，
分别是
的中点，
分别是
的中点，
（Ⅰ）求证：
面
；
（Ⅱ）求二面角
的大小。
全国卷（Ⅰ）文
一、选择题(每题5分)
（9）已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的
表面积是( )
（A）16π （B）20π （C）24π （D）32π
二、填空题(每题4分)
(14)已知正四棱锥的体积为12，底面对角线的长为
，则侧面与底面所成的
二面角等于
三、解答题
(20) (本小题满分12分)
如图，l
、l
是互相垂直的异面直线，MN是它们的公垂线段.点A、B在上l，
C在l上,AM=MB=MN.
（Ⅰ）证明AC
；
（Ⅱ）若
，求NB与平面ABC所成角的余弦值.
全国卷（Ⅱ）文
一、选择题（每小题5分）
（7）如图，平面
平面
，
与两平面
、
所成的角
分别为
和。过A、B分别作两平面交线的垂线，垂足为
、若AB=12,
则
（）
（A）4 （B）6 （C）8 （D）9
二、填空题（每小题4分）
（14）圆
是以
为半径的球的小圆，若圆的面积
和球
的表面积
的
比为
，则圆心
到球心
的距离与球半径的比
＿＿＿＿＿。
三、解答题
（20）（本小题１２分）
如图，在直三棱柱
中，
、
分别为
、
的中点。
（I）证明：ED为异面直线
与
的公垂线；
（II）设
求二面角
的大小
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。
