三、解答题
19.(本小题满分12分)
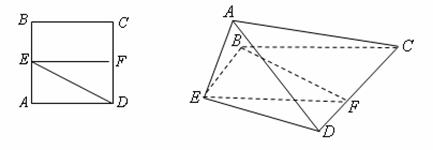
已知正方形![]() ,
,![]() 分别是边
分别是边![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,
折起,
如图所示,记二面角![]() 的大小为
的大小为![]() (
(![]() ).
).
(1)证明![]() 平面
平面![]() ;
;
(2)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的射影
内的射影![]() 是否在直线
是否在直线
![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的余弦值.
的余弦值.
(19)本小题主要考查空间中的线面关系,解三角形等基础知识,考查空间想象能力
和思维能力.满分12分.
(Ⅰ)证明:E、F分别是正方形ABCD的边AB、CD的中点.
∴EB∥FD,且EB=FD.
∴四边形EBFD是平行四边形,
∴BF∥ED.
∵ED![]() 平面AED.而BF
平面AED.而BF![]() 平面AED,
平面AED,
∴BF∥平面AED.
(Ⅱ)解法一:点A在平面BCDE内的射影G在直线EF上.
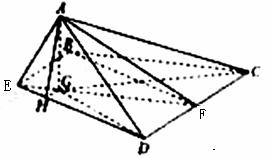
过点A作AG⊥平面BCDE,垂足为G,连结GC,GD.
∵△ACD为正三角形,
∴AC=AD.
∴GC=GD.
∴G在CD的垂直平分线上.
又∵EF是CD的垂直平分线,
∴点A在平面BCDE内的射影G在直线EF上.过G作GH⊥ED,垂足为H,连结AH,即AH⊥DE.
∴∠AHG是二面角A-DE-C的平面角,即∠AHG=θ
设原正方形ABCD的边长为2a,连结AF.
在折后图的△AEF中,AF=![]() a,EF=2AE=2a,
a,EF=2AE=2a,
∴△AEF为直角三角形,AG·EF=AE·AF,
∴AG=![]() a.
a.
在Rt△ADE中,AH·DE=AD·AE,
∴AH=![]() ,
,
∴GH=![]() ,
,
∴cosθ=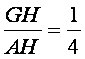 .
.
解法二:点A在平面BCDE内的射影G在直线EF上.

连结AF,在平面AEF内过点A作AG′⊥EF,垂足为G′.
∵△ACD为正三角形,F为CD的中点,
∴AF⊥CD.
又∵EF⊥CD,
∴CD⊥平面AEF.
∵AG′![]() 平面AEF,
平面AEF,
∴CD⊥AG′.
又∵AG′⊥EF,且CD∩EF=F,CD![]() 平面BCDE,EF
平面BCDE,EF![]() 平面BCDE,
平面BCDE,
∴AG′⊥平面BCDE,
∴G′为A在平面BCDE内的射影G.
∴点A在平面BCDE内的射影G在直线EF上.
过G作GH⊥ED,垂足为H,连结AH,则AH⊥DE,
∴∠AHG是二面角A-DE-C的平面角,即∠AHG=θ
设原正方形ABCD的边长为2a.
在折后图的△AEF中,AF=![]() a,EF=2AE=2a,
a,EF=2AE=2a,
∴△AEF为直角三角形,AG·EF=AE·AF.
∴AG=![]() a,
a,
在Rt△ADE中,AH·DE=AD·AE,
∴AH=![]() ,
,
∴GH=![]() ,
,
∴cosθ=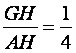 .
.
解法三:点A在平面BCDE内的射影G在直线EF上.连结AF,在平面AEF内过点A作AG′⊥EF,垂足为G′.
∵△ACD为正三角形,F为CD中点.
∴AF⊥CD.
又∵EF⊥CD.
∴CD⊥平面AEF.
∵CD![]() 平面BCDE,
平面BCDE,
∴平面AEF⊥平面BCDE.
又∵平面AEF∩平面BCDE=EF,AG′⊥EF,
∴AG′⊥平面BCDE,即G′为A在平面BCDE内的射影G,
∴点A在平面BCDE内的射影G在直线EF上.
过G作GH⊥DE,垂足为H,连结AH,则AH⊥DE,
∴∠AHG是二面角A-DE-C的平面角,即∠AHG=θ.
设原正方形ABCD的边长为2a.
在折后图的△AEF中,AF=![]() a,EF=2AE=2a,
a,EF=2AE=2a,
∴△AEF为直角三角形,AG·EF=AE·AF.
∴AG=![]() a.
a.
在Rt△ADE中,AH·DE=AD·AE,
∴AH=![]() ,
,
∴GH=![]() ,
,
∴cosθ=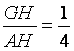 .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。