三、解答题
20.(本小题满分12分)
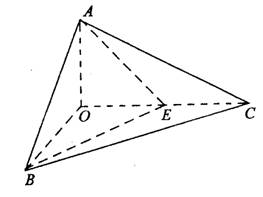
如图,已知三棱锥O-ABC的侧棱OA、OB、OC两两垂直,且OA=1,OB=OC=2,
E是OC的中点.

(1)求O点到面ABC的距离;
(2)求异面直线BE与AC所成的角;
(3)求二面角E-AB-C的大小.
20.(1)取BC的中点D,连AD、OD,
∵OB=OC,则OD⊥BC、AD⊥BC,
∴BC⊥面OAD.过O点作OH⊥AD于H,
则OH⊥面ABC,OH的长就是所要求的距离.
BC=2![]() ,OD=
,OD=![]() .
.
∵OA⊥OB、OA⊥OC,
∴OA⊥面OBC,则OA⊥OD.
AD=![]() ,在直角三角形OAD中,有OH=
,在直角三角形OAD中,有OH= .
.
(另解:由V=![]() S△ABC·OH=
S△ABC·OH=![]() OA·OB·OC=
OA·OB·OC=![]() 知:OE=
知:OE=![]() .)
.)
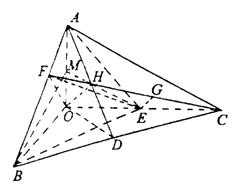
(2)取OA的中点M,连EM、BM,则EM∥AC,∠BEM是异面直线BE与AC所成的角.
求得:EM= ,BE=
,BE=![]() ,BM=
,BM= .
.
cos∠BEM=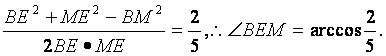
(3)连结CH并延长交AB于F,连结OF、EF.
∵OC⊥面OAB,∴OC⊥AB.又∵OH⊥面ABC,∴CF⊥AB,EF⊥AB,
则∠EFC就是所求二面角的平面角.作EG⊥CF于G,则EG=![]() OH=
OH=![]() .
.
在直角三角形OAB中,OF=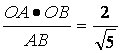 ,
,
在直角三角形OEF中,EF= ,
,
sin∠EFG=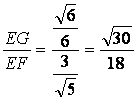 ,∠EFG=arcsin
,∠EFG=arcsin![]() .(或表示为arccos
.(或表示为arccos![]() )
)
方法二:(1)以O为原点,OB、OC、OA分别为x、y、z轴建立空间直角坐标系.
则有A(0,0,1)、B(2,0,0)、C(0,2,0)、E(0,1,0).
设平面ABC的法向量为![]() =(x,y,z),
=(x,y,z),
则由![]() 知:
知:![]() =2x-z=0;
=2x-z=0;
由![]() 知:
知:![]() =2y-z=0.取
=2y-z=0.取
![]() =(1,1,2),则点O到面ABC的距离为
=(1,1,2),则点O到面ABC的距离为
d= .
.

(2)![]() =(2,0,0)-(0,1,0)=(2,-1,0),
=(2,0,0)-(0,1,0)=(2,-1,0),
![]() =(0,2,-1).
=(0,2,-1).
cos<![]() ,
,![]() >=
>= ,所以异面直线BE与AC所成的角arccos
,所以异面直线BE与AC所成的角arccos![]() .
.
(3)设平面EAB的法向量为![]() =(x,y,z),则由
=(x,y,z),则由![]() ⊥
⊥![]() 知:
知:![]() ·
·![]() =2x-z=0;
=2x-z=0;
由![]() ⊥
⊥![]() 知:
知:![]() ·
·![]() =2x-y=0.取
=2x-y=0.取![]() =(1,2,2).
=(1,2,2).
由(1)知平面ABC的法向量为![]() =(1,1,2).
=(1,1,2).
cos<![]() ,
,![]() >=
>=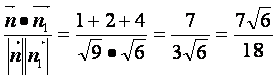 ,
,
结合图形可知,二面角E-AB-C的大小为:arccos![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。