三、解答题

18．（本小题满分12分）

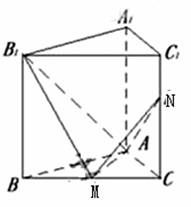
如图，已知正三棱柱ABC—A₁B₁C₁的侧棱长和底面边长为1，M是底面BC边上的中点，

N是侧棱CC₁上的点，且CN=2C₁N。

（Ⅰ）求二面角B₁—AM—N的平面角的余弦值；

（Ⅱ）求点B₁到平面AMN的距离。

    本小题主要考查线面关系、二面角和点到平面距离的有关知识及空间想象能力

和推理运算能力.考查应用向量知识解决数学问题的能力.

解法1：（Ⅰ）因为M是底面BC边上的中点，所以AM⊥BC，又AM⊥CC₁，所以AM⊥面

BCC₁B₁.从而AM⊥B₁M，AM⊥NM，所以∠B₁MN为二面角B₁—AM—N的平面角.

又B₁M=，

MN=，

连B₁N，得B₁N=.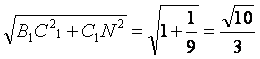

在△B₁MN中，由余弦定理得

cosB₁MN=

=

=.

故所求二面角B₁—AM—N的平面角的余弦值为.

（Ⅱ）过B₁在面BCC₁B₁内作直线B₁H⊥MN，H为垂足.

又AM⊥面BCC₁B₁，所以AM⊥B₁H.

于是B₁H⊥平面AMN，故B₁H即为B₁到平面AMN的距离.

在RT△B₁HM中，B₁H=B₁MsinB₁MH==1.

故点B₁到平面AMN的距离为1.

解法2：（Ⅰ）建立如图所示的空间直角坐标系，则B₁（0，0，1）M（0，，0）

，C（0，1，0），N（0，1，），A（－，，0）.所以，=（，0，0）

，=（0，－，1），=（0，，）.

因为·=×0+0×（-）+0×1=0所以⊥.同法可得⊥.

故<，>为二面角B₁—AM—N的平面角.

∴cos＜，＞=.

故所求二面角B₁—AM—N的平面角的余弦值为.

（Ⅱ）设n=（x，y，z）为平面AMN的一个法向量，则由n⊥，n⊥得

故可取n=（0，－，1）

设与n的夹角为α，则cosα=.

所以B₁到平面AMN的距离为||·|cosα|==1.