三、解答题
(20)(本小题满分12分)
如图,在正四棱柱ABCD-A1B1C1D1中:AB=1,BB1=![]() +1,E为BB1上
+1,E为BB1上
使B1E=1的点,平面AEC1交DD1于F,交A1D1的延长线于G.求:
(Ⅰ)异面直线AD与C1G所成的角的大小;
(Ⅱ)二面角A-C1G-A1的正切值.

(本小题12分)

解法一:
(Ⅰ)由AD∥D1G知∠C1GD1为异面直线AD与C1G所成的角.
连接C1F。因为AE和C1F分别是平行平面ABB1A1和CC1D1D
与平面AEC1G的交线,所以AE∥C1F,由此可得D1F=BE=![]() .
.
再△FD1G∽△FDA得D1G=![]() .
.
在Rt△C1D1G中,由C1D1=1,D1G=![]() 得∠C1GD1=
得∠C1GD1=![]() .
.
(Ⅱ)作D1H⊥C1G于H,连接FH,由三垂线定理知FH⊥C1G,
故∠D1HF为二面角F-C1G-D1即二面角A-C1G-A1的平面角.
在Rt△GHD1中,由D1G=![]() ,∠D1GH=
,∠D1GH=![]() 得D1H=
得D1H=![]() .从而
.从而
tanD1HF=
解法二:

(Ⅰ)由AD∥D1G知∠C1GD1为异面直线AD与C1G所成的角.
因为EC1和AF是平行平面BB1C1C与AA1D1D与平面AEC1G的交线,
所以EC1∥AF.
由此可得∠AGA1=∠EC1B1=![]() ,
,
从而A1G=AA1=![]() ,于是D1G=
,于是D1G=![]()
在Rt△C1D1G中,由C1D1=1,D1G=![]() 得∠C1GD1=
得∠C1GD1=![]()
(Ⅱ)在△A1C1G中,由∠C1A1G=![]() ,∠A1GC1=
,∠A1GC1=![]() 知∠A1C1G为钝角,
知∠A1C1G为钝角,
作A1H⊥GC1交GC1的延长线于H,连接AH.由三垂线定理知GH⊥AH,
故∠AHA1为二面角A-C1G-A1的平面角.
在Rt△A1HG中,由A1C=![]() ,∠A1GH=
,∠A1GH=![]() 得A1H=
得A1H=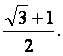
从而
tanAHA1=
解法三:
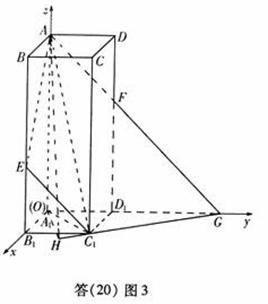
(Ⅰ)以A1为原点,A1B1,A1D1,A1A所在直线分别为x轴,
y轴和z轴建立如图所示的空间直角坐标系.于是,A(0,0,![]() +1),
+1),
C1(1,1,0),D(0,1,![]() +1),E(1,0,1)、
+1),E(1,0,1)、![]() =(0,1,0),
=(0,1,0),
![]() =(0,1,-1)
=(0,1,-1)
因为EC1和AF分别是平行平面BB1C1C和AA1D1D与平面AEC1G的交线,
所以EC1∥AF,设G(0,y,0),
则![]()
由![]() ∥
∥![]() 得
得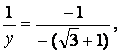 于是y=
于是y=![]() +1.
+1.
故G(0,![]() +1,0)
+1,0)![]() (-1,
(-1,![]() ,0).
,0).
设异面直线AD与C1G所成的角的大小为θ,则

从而
θ=![]()
(Ⅱ)作A1H⊥C1G于H.由三垂线定理知AH⊥CH,故∠AHA1为
二面角A-C1G-A1的平面角.
设H(a,b,0),则![]()
由A1H⊥C1G得![]() ,由此得a-
,由此得a-![]() b=0.
①
b=0.
①
又由H1C1,G共线得![]() ∥
∥![]() ,从而
,从而 于是
于是
![]() ②
②
联立①和②得a=
由| 得
得
tan AHA1=
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。