三、解答题

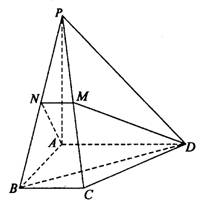
(17)如图，在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD=90°，

PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点．

    (Ⅰ)求证：PB⊥DM；

    (Ⅱ)求BD与平面ADMN所成的角．

本题主要考查空间线线、线面关系、空间向量的概念与运算等基础知识，

同时考查空间想象能力。满分14分。

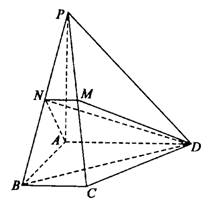
解：方法一：

       (Ⅰ)因为N是PB的中点，PA=AB，

          所以AN⊥PB．

          因为AD⊥面PAB，

          所以AD⊥PB．

          从而PB⊥平面ADMN．

          因为DM平面ADMN，

          所以PB⊥DM．

       (Ⅱ)连结DN，

          因为PB⊥平面ADMN，

          所以∠BDN是BD与平面ADMN所成的角．

          在Rt△BDN中，

          sin∠BDN=，

          故BD与平面ADMN所成的角是.

方法二：

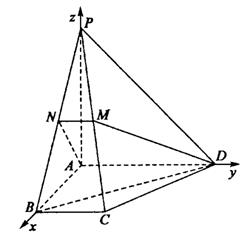
   如图，以A为坐标原点建立空间直角坐标系A-xyz，设BC=1，

则A（0，0，0），P（0，0，2），B（2，0，0），M（1，，1），

D（0，2，0）.

   (Ⅰ)因为

               =0，

      所以PB⊥DM.

  (Ⅱ)因为

              =0,

     所以PB⊥AD.

     又PB⊥DM,

     所以PB⊥平面ADMN.

     因此的余角即是BD与平面ADMN所成的角.

     因为

     cos=

                   =

     所以=.

     因此BD与平面ADMN所成的角为