三、解答题

（１９）（本小题满分１２分）

如图，点A在直线上的射影为点B在上的射影为

已知求：

       （I）直线AB分别与平面所成角的大小；

       （II）二面角的大小。

(第19题图)

解法一：（Ⅰ）如图，连接A₁B，AB_1,

∵α⊥β，α∩β=l，AA₁⊥l,BB₁⊥l，  ∴AA₁⊥β，BB₁⊥α，

则∠BAB₁，∠ABA₁分别是AB与α和β所成的角.

Rt△BB₁A中，BB₁=，AB=2，

∴sin∠BAB₁=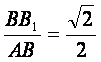,        ∴∠BAB₁=45°.

Rt△AA₁B中，AA₁=1，AB=2.

∴sin∠ABA₁=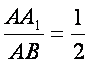,        ∴∠ABA₁=30°.

故AB与平面α,β所成的角分别是45°，30°.

（Ⅱ）∵BB₁⊥α，       

∴平面ABB₁⊥α，在平面α内过A₁作A₁E⊥AB₁交AB₁于E，则A₁E⊥平面AB₁B.

过E作EF⊥AB交AB于F，连接A₁F，则由三垂线定理得A₁F⊥AB，∴∠A₁FE就

是所求二面角的平面角.

在Rt△ABB₁中，∠BAB₁=45°，∴AB₁=B₁B=.

∴Rt△AA₁B₁中，AA₁=A₁B₁=1，∴A₁E=AB₁=.

在Rt△AA₁B中，A₁B=.  由AA₁·A₁B=A₁F，AB得

A₁F=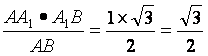.      ∴在Rt△A₁EF中，sin∠A₁FE==.

∴二面角A₁－AB－B₁的大小为arcsin.

解法二：（Ⅰ）同解法一.

(Ⅱ)如图，建立坐标系，则A₁（0，0，0），A（0，0，1），

B₁（0，1，0）B（，1，0）.

在AB上取一点F（x,y,z），则存在t∈R，使得=t，

即  （x,y,z－1）=t(),∴点F的坐标为(t,t,1－t).

要使   ，须=0.

即（,t,1－t）·（,1,－1）=0，2t+t－(1－t)=0，解得t=,

∴点F的坐标为().∴().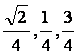

设E为AB₁的中点，则点E的坐标为（0，）.

∴

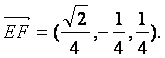
又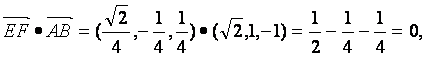

∴，     ∴∠A₁FE为所求二面角的平面角.

又cos∠A₁FE,

           .

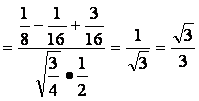∴二面角A₁－AB－B₂的大小为arccos.