三、解答题

(17)(本小题共14分)

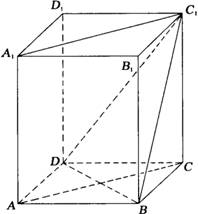
如图，ABCD-A₁B₁C₁D₁是正四棱柱.

(Ⅰ)求证：BD⊥平面ACC₁A₁；

(Ⅱ)若二面角C₁-BD-C的大小为60°，求异面直线BC₁与AC所成角的大小.

解法一：

(Ⅰ)∵ABCD-A₁B₁C₁D₁是正四棱柱，

∴CC₁⊥平面ABCD，

∴BD⊥CC₁.

∵ABCD是正方形,

∴BD⊥AC.

又∵AC，CC₁平面ACC₁A₁，且AC∩CC₁=C，

∴BD⊥平面ACC₁A₁.

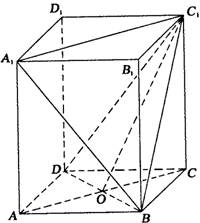
(Ⅱ)设BD与AC相交于O，连接C₁O.

∵CC₁⊥平面ABCD，BD⊥AC，

∴BD⊥C₁O，

∴∠C₁OC是二面角C₁-BD-C的平面角，

∴∠C₁OC=60°.

连接A₁B.

∵A₁C₁∥AC，

∴∠A₁C₁B是BC₁与AC所成角.

设BC=a，则CO=a，CC₁=CO·tan60°=a，A₁B=BC₁=a，

A₁C₁=a.

在△A₁BC₁中，由余弦定理得

cosA₁C₁B=，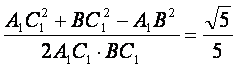

∴∠A₁C₁B=arccos，

∴异面直线BC₁与AC所成角的大小为arccos.

解法二：

(Ⅰ)建立空间直角坐标系D-xyz，如图.

设AD=a，DD₁=b，则有D(0，0，0)，A(a，0，0)，B(a，a，0)，C(0，a，0)，C₁(0，a，b)，

∴=(-a，-a，0)，=(-a，a，0)，=(0，0，b)，

∴·=0，·=0，

∴BD⊥AC，BD⊥CC₁.

又∵AC，CC₁平面ACC₁A₁，且AC∩CC₁=C，

∴BD⊥平面ACC₁A₁.

(Ⅱ)设BD与AC相交于O，连接C₁O，则点O坐标为()，=(-).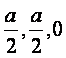

∵=0，

∴BD⊥C₁O，又BD⊥CO，

∴∠C₁OC是二面角C₁-BD-C的平面角，

∴∠C₁OC=60°.

∵tanC₁OC=，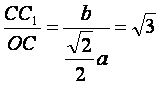

∴b=a.

∵=(-a，a，0)，=(-a，0，b)，

∴cos<,>=.

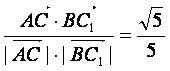∴异面直线BC₁与AC所成角的大小为arccos.