已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，
底面ABCD，解答题
全国卷Ⅰ(理)
2004年
18．（本小题满分12分）
一接待中心有A、B、C、D四部热线电话，已知某一时刻电话A、B占线的
概率均为0.5，电话C、D占线的概率均为0.4，各部电话是否占线相互之间
没有影响.假设该时刻有ξ部电话占线.试求随机变量ξ的概率分布和它的期望.
2005年
（18）（本大题满分12分）
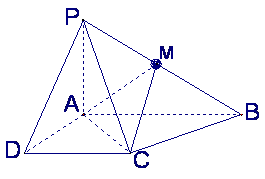
已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，底面ABCD，
且PA=AD=DC=
AB=1，M是PB的中点
（Ⅰ）证明：面PAD⊥面PCD；
（Ⅱ）求AC与PB所成的角；
（Ⅲ）求面AMC与面BMC所成二面角的大小
2006年
（18）（本小题满分12分）
A、B是治疗同一种疾病的两种药，用若干试验组进行对比试验.每个试验组由4只
小白鼠组成，其中2只服用A，另2只服用B，然后观察疗效，若在一个试验组中，
服用A有效的小白鼠的只数比服用B有效的多，就称该试验组为甲类组，设每只小
白鼠服用A有效的概率为
，服用B有效的概率为
。
（Ⅰ）求一个试验组为甲类组的概率。
（Ⅱ）观察3个试验组，用
表示这3个试验组中甲类组的个数，求
的分布列和数
学期望。
2007年
（18）（本小题满分12分）
某商场经销某商品，根据以往资料统计，顾客采用的付款期数
的分布列为
|
|
1 |
2 |
3 |
4 |
5 |
|
|
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品，采用1期付款，其利润为200元；分2期或3期付款，其利润
为250元；分4期或5期付款，其利润为300元．
表示经销一件该商品的利润．
（Ⅰ）求事件
：“购买该商品的3位顾客中，至少有1位采用1期付款”的概率
；
（Ⅱ）求
的分布列及期望
．
全国卷Ⅱ(理)
2004年
18．（本小题满分12分）
已知8支球队中有3支弱队，以抽签方式将这8支球队分为A、B两组，每组4支.
求：（Ⅰ）A、B两组中有一组恰有两支弱队的概率；
（Ⅱ）A组中至少有两支弱队的概率.
2005年
（18） （本小题满分12分）
已知
是各项均为正数的等差数列，
、
、
成等差数列．又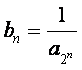
，
…
（Ⅰ）证明
为等比数列；
（Ⅱ）如果无穷等比数列各项的和
，求数列
的首项
和公差
．
（注：无穷数列各项的和即当
时数列前项和的极限）
2006年
（18）（本小题满分１２分）
某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，
再从每箱中任意抽取2件产品进行检验。设取出的第一、二、三箱中
分别有0件、1件、2件二等品，其余为一等品。
（I）用
表示抽检的6件产品中二等品的件数，求的分布列及的数学期望；
（II）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，
求这批产品被用户拒绝购买的概率。
2007年
18．（本小题满分12分）
从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件
：
“取出的2件产品中至多有1件是二等品”的概率
．
（1）求从该批产品中任取1件是二等品的概率
；
（2）若该批产品共100件，从中任意抽取2件，表示取出的2件产品中
二等品的件数，求
的分布列．
全国卷Ⅲ(理)
2004年
18．（本小题满分12分）解方程
.
2005年
18.（本小题满分12分）
四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，
平面VAD⊥底面ABCD
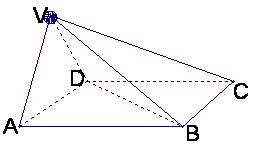1）求证AB⊥面VAD；
2）求面VAD与面VDB所成的二面角的大小．
全国卷Ⅳ(理)
2004年
18．（本小题满分12分）
求函数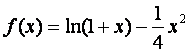
在[0，2]上的最大值和最小值.
2007年
北京卷(理)
2004年
（16）（本小题满分14分）
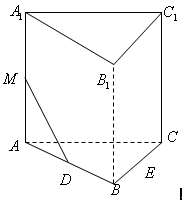
如图，在正三棱柱
中，AB＝3，
，M为
的中点，P是BC上一点，
且由P沿棱柱侧面经
过棱
到M的最短路线长为
，设这条最短路线与
的交点为N，
求：
（I）该三棱柱的侧面展开图的对角线长
（II）PC和NC的长
（III）平面NMP与平面ABC所成二面角（锐角）的大小（用反三角函数表示）
2005年
16 (本小题共14分)
如图,在直四棱柱
中,
,
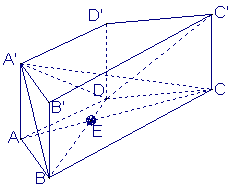
垂足为
(Ⅰ)求证
;
(Ⅱ)求二面角
的大小;
(Ⅲ)求异面直线
与
所成角的大小
2006年
（16）（本小题共13分）
已知函数f（x）=ax3+bx2+cx在点x0处取得极大值5，其导函数y=f′（x）
的图象经过点（1，0），（2，0），如图所示，求：
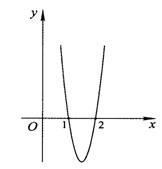
（Ⅰ）x0的值；
（Ⅱ）a，b，c的值.
2007年
16．（本小题共14分）
如图，在
中，
，斜边
．
可以通过
以
直线
为轴旋转得到，且二面角
是直二面角．动点
的斜边
上．
（I）求证：平面
平面
；
（II）当
为的中点时，求异面直线
与
所成角的大小；
（III）求
与平面
所成角的最大值．
天津卷(理)
2004年
18. （本小题满分12分）
从4名男生和2名女生中任选3人参加演讲比赛，设随机变量表示
所选3人中女生的人数。
（1）求的分布列；
（2）求的数学期望；
（3）求“所选3人中女生人数
”的概率。
2005年
（18）（本小题满分12分）
已知
（Ⅰ）当
时，求数列
的前n项和
（Ⅱ）求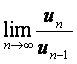
2006年
(18)(本小题满分12分)
某射手进行射击训练，假设每次射击击中目标的概率为
，
且各次射击的结果互不影响．
(Ⅰ)求射手在3次射击中，至少有两次连续击中目标的概率(用数字作答)；
(Ⅱ)求射手第3次击中目标时，恰好射击了4次的概率(用数字作答)；
(Ⅲ)设随机变量ξ表示射手第3次击中目标时已射击的次数，求ξ的分布列．
2007年
18．（本小题满分12分）
已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的2个红球和
4个黑球．现从甲、乙两个盒内各任取2个球．
（Ⅰ）求取出的4个球均为黑球的概率；
（Ⅱ）求取出的4个球中恰有1个红球的概率；
（Ⅲ）设为取出的4个球中红球的个数，求的分布列和数学期望．
上海卷(理)
2004年
18、(本题满分12分)
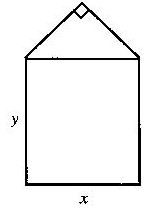某单位用木料制作如图所示的框架,
框架的下部是边长分别为
x、y(单位：m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm2.
问x、y分别为多少(精确到0.001m) 时用料最省?
2005年
18.证明：在复数范围内，方程
（
为虚数单位）无解
2006年
18．（本题满分12分）
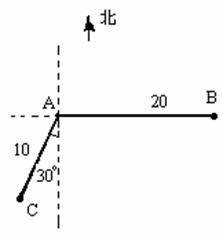
如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘
渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南
偏西30
，相距10海里C处的乙船，试问乙船应朝北偏东多少度的方向
沿直线前往B处救援（角度精确到1）？
2007年
17．（本题满分14分）
在
中，
分别是三个内角
的对边．若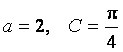
，
，
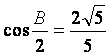求
的面积
．
辽宁卷（理）
2004年
18．（本小题满分12分）
设全集U=R
（1）解关于x的不等式
（2）记A为（1）中不等式的解集，集合
，
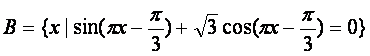若（ ∪A）∩B恰有3个元素，求a的取值范围.
2005年
18．（本小题满分12分）
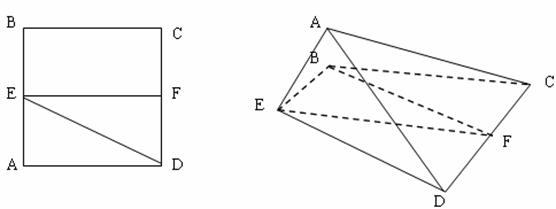
如图，在直径为1的圆O中，作一关于圆心对称、
邻边互相垂直的十字形，其中
（Ⅰ）将十字形的面积表示为
的函数；
（Ⅱ）为何值时，十字形的面积最大？最大面积是多少？
2006年（理）
(18) (本小题满分12分)
已知正方形
.
、
分别是
、
的中点,将
沿
折起,如图
所示,记二面角
的大小为
.
( I)
证明
平面
;
( II)若
为正三角形,试判断点
在平面
内的射影
是
否在直线
上,证明你的结论,并求角
的余弦值.
2007年
18．（本小题满分12分）
如图，在直三棱柱
中，
，
，
分别为棱
的中点，
为棱
上的点，二面角
为
．
（I）证明：
；
（II）求
的长，并求点
到平面
的距离．
江苏卷
2004年
18.在棱长为4的正方体ABCD-A1B1C1D1中，O是正方形A1B1C1D1的中心，
点P在棱CC1上，且CC1=4CP.
(Ⅰ)求直线AP与平面BCC1B1所成的角的大小（结果用反三角函数值表示）；
(Ⅱ)设O点在平面D1AP上的射影是H，求证：D1H⊥AP；
(Ⅲ)求点P到平面ABD1的距离.
2005年
20.（本小题满分12分，每小问满分4分）甲.乙两人各射击一次，
击中目标的概率分别是
和
假设两人射击是否击中目标，相互之间没有影响；
每人各次射击是否击中目标，相互之间也没有影响
⑴求甲射击4次，至少1次未击中目标的概率；
⑵求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；
⑶假设某人连续2次未击中目标，则停止射击问：乙恰好射击5次后，被中止
射击的概率是多少？
2006年
（18）（本小题满分14分）
请您设计一个帐篷。它下部的形状是高为1m的正六棱柱，上部的形状是
侧棱长为3m的正六棱锥（如右图所示）。试问当帐篷的顶点O到底面中
心
的距离为多少时，帐篷的体积最大？
2007年
18．（本题满分12分）
如图，已知
是棱长为
的正方体，
点
在
上，点
在
上，且
．
（1）求证：
四点共面；（4分）
（2）若点
在
上，
，点
在上，
，垂足为
，求证：
平面
；（4分）
（3）用
表示截面
和侧面所成的锐二面角的大小，求
．（4分）
浙江卷(理)
2004年
（18） （本题满分12分）
盒子中有大小相同的球10个，其中标号为1的球3个，标号为2的球4个，
标号为5的球3个，第一次从盒子中任取1个球，放回后第二次再任取1个球
（假设取到每个球的可能性都相同）。记第一次与第二次取到球的标号之和为ε。
（Ⅰ）求随机变量ε的分布列；
（Ⅱ）求随机变量ε的期望Eε。
2005年
16．已知函数f(x)和g(x)的图象关于原点对称，且f(x)＝x2＝2x．
(Ⅰ)求函数g(x)的解析式；
(Ⅱ)解不等式g(x)≥f(x)－|x－1|．
2006年
（16）设
：
（Ⅰ）
;
（Ⅱ）方程
在（0，1）内有两个实根。
2007年
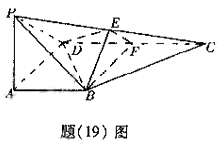
（19）（本题14分）在如图所示的几何体中，
平面
，
平面，
，且
，是
的中点．
（I）求证：
；
（II）求
与平面
所成的角．
福建卷(理)
2004年
（18）（本小题满分12分）
甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能
答对其中的6题，乙能答对其中的8题。规定每次考试都从备选题中随
机抽出3题进行测试，至少答对2题才算合格。
（Ⅰ）求甲答对试题数ξ的概率分布及数学期望；
（Ⅱ）求甲、乙两人至少有一人考试合格的概率。
2005年
18．（本小题满分12分）
甲、乙两人在罚球线投球命中的概率分别为
，投中得1分，投不中得0分.
（Ⅰ）甲、乙两人在罚球线各投球一次，求两人得分之和ξ的数学期望；
（Ⅱ）甲、乙两人在罚球线各投球二次，求这四次投球中至少一次命中的概率；
2006年
（18）（本小题满分12分）
如图，四面体ABCD中，O、E分别是BD、BC的中点，
（I）求证：
平面BCD；
（II）求异面直线AB与CD所成角的大小；
（III）求点E到平面ACD的距离。
2007年
18．（本小题满分12分）
如图，正三棱柱
的所有棱长都为
，
为
中点．
（Ⅰ）求证：
平面
；
（Ⅱ）求二面角
的大小；
C1
（Ⅲ）求点
到平面
的距离．
B1
湖北卷(理)
2004年
（18）（本小题满分12分）
如图，在棱长为1的正方体ABCD－A1、B1、C1、D1中，点E是棱BC的中点，
点F 是棱CD上的动点。
（Ⅰ）试确定点F的位置，使得D1E⊥平面AB1F；
（Ⅱ）当D1E⊥平面AB1F时，求二面角C1―EF―A的大小
（结果用反三角函数值表示）。
2005年
18．（本小题满分12分）
在ΔABC中，已知
，AC边上的中线BD=
，求sinA的值
2006年
17．（本小题满分13分）
已知二次函数y=f(x)的图象经过坐标原点，其导函数为
.数列{
}的
前n项和为Sn，点
均在函数y=f(x)的图象上。
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设
，Tn是数列{bn}的前n项和，求使得Tn＜
对所有
都成
立的最小正整数m。
2007年
17．（本小题满分12分）
在生产过程中，测得纤维产品的纤度（表示纤维粗细的一种量）共有100个数据，
将数据分组如表：
|
分组 |
频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
（I）在答题卡上完成频率分布表，并在给定的坐标系
中画出频率分布直方图；
（II）估计纤度落在
中的概率及纤度小于
的概率是多少？
（III）统计方法中，同一组数据常用该组区间的中点值
（例如区间
的中点值是
）作为代表．据此，
估计纤度的期望．
湖南卷(理)
2005年
17．（本题满分12分）
如图1，已知ABCD是上．下底边长分别为2和6，高为
的等腰梯形，
将它沿对称轴OO1折成直二面角，如图2.
（Ⅰ）证明：AC⊥BO1；
（Ⅱ）求二面角O－AC－O1的大小.
2006年
17．(本小题满分12分)
某安全生产监督部门对5家小型煤矿进行安全检查(简称安检)．若安检不合格，
则必须整改．若整改后经复查仍不合格，则强制关闭．设每家煤矿安检是否合格
是相互独立的，且每家煤矿整改前安检合格的概率是0.5，整改后安检合格的概率
是0.8，计算(结果精确到0.01)：
(Ⅰ)恰好有两家煤矿必须整改的概率；
(Ⅱ)平均有多少家煤矿必须整改；
(Ⅲ)至少关闭一家煤矿的概率．
图1
图2
2007年
17．（本小题满分12分）
某地区为下岗人员免费提供财会和计算机培训，以提高下岗人员的再就业能力，
每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训，已知参加
过财会培训的有60%，参加过计算机培训的有75%，假设每个人对培训项目的选
择是相互独立的，且各人的选择相互之间没有影响．
（I）任选1名下岗人员，求该人参加过培训的概率；
（II）任选3名下岗人员，记
为3人中参加过培训的人数，求的分布列和期望．
广东卷（理）
2004年
18. (12分)如右下图,在长方体ABCD—A1B1C1D1中,已知AB= 4, AD =3, AA1= 2.
E、F分别是线段AB、BC上的点，且EB= FB=1.
(1)
求二面角C—DE—C1的正切值;
(2) 求直线EC1与FD1所成的余弦值.
2005年
16．（本小题满分14分）
如图3所示，在四面体P—ABC中，已知PA=BC=6，PC=AB=10，AC=8，PB=
.
F是线段PB上一点，
，点E在线段AB上，且EF⊥PB.
（Ⅰ）证明：PB⊥平面CEF；
（Ⅱ）求二面角B—CE—F的大小.
2006年
16．（本小题满分12分）
某运动员射击一次所得环数X的分布如下：
|
X |
0-6 |
7 |
8 |
9 |
10 |
|
p |
0 |
0.2 |
0.3 |
0.3 |
0.2 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为
。
（Ⅰ）求该运动员两次都命中7环的概率：
（Ⅱ）求
的分布列：
（Ⅲ）求的数学期望E
。
2007年
17．（本小题满分12分）
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
（吨）与
相应的生产能耗（吨标准煤）的几组对照数据．
|
|
3 |
4 |
5 |
6 |
|
|
2.5 |
3 |
4 |
4.5 |
（1）请画出上表数据的散点图；
（2）请根据上表提供的数据，用最小二乘法求出
关于
的线性回归方程
；
（3）已知该厂技改前
吨甲产品的生产能耗为
吨标准煤．试根据（2）求出
的线性回归方程，预测生产吨甲产品的生产能耗比技改前降低多少吨标准煤？
（参考数值：
）
重庆卷(理)
2004年
18．（本小题满分12分）
设一汽车在前进途中要经过4个路口，汽车在每个路口遇到绿灯的
概率为
，遇到红灯（禁止通行）的概率为。假定汽车只在遇到
红灯或到达目的地才停止前进，表示停车时已经通过的路口数，求：
（1）的概率的分布列及期望E;
(2 ) 停车时最多已通过3个路口的概率。
2005年
18．（本小题满分13分）
在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；
有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖，某顾客从此10张券
中任抽2张，求：
（Ⅰ）该顾客中奖的概率；
（Ⅱ）该顾客获得的奖品总价值（元）的概率分布列和期望
2006年
（18）（本小题满分13分）
某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠。若该
电梯在底层载有5位乘客，且每位乘客在这三层的每一层下电梯的概率均
为
，用表示这5位乘客在20层下电梯的人数，求：
（Ⅰ）随即变量
的分布列；
（Ⅱ）随即变量
的期望；
2007年
18．（本小题满分13分，其中（Ⅰ）小问4分，（Ⅱ）小问9分）
某单位有三辆汽车参加某种事故保险，单位年初向保险公司缴纳每辆
元的保险金，
对在一年内发生此种事故的每辆汽车，单位可获元的赔偿（假设每辆车最多只赔
偿一次），设这三辆车在一年内发生此种事故的概率分别为，
，
，且各车是否
发生事故相互独立，求一年内该单位在此保险中：
（Ⅰ）获赔的概率；
（Ⅱ）获赔金额的分布列与期望．
山东卷(理)
2005年
(18) （本小题满分12分）
袋中装有罴球和白球共7个,从中任取2个球都是白球的概率为
.现有甲、乙
两人从袋中轮流摸取1个球，甲先取，乙后取，然后甲再取
取后不放回，
直到两人中有一人取到白球时即终止
每个球在每一次被取出的机会是等可能的，
用表示取球终止时所需的取球次数．
（Ⅰ）求袋中原有白球的个数；
（Ⅱ）求随机变量的概率分布；
（Ⅲ）求甲取到白球的概率
2006年
18．(本小题满分12分)
设函数f(x)=ax-(a+1)ln(x+1)，其中a≥-1．求f(x)的单调区间．
2007年
（18）（本小题满分12分）
设和
分别是先后抛掷一枚骰子得到的点数，用随机变量表示方程
实根的个数（重根按一个计）．
（Ⅰ）求方程
有实根的概率；
（Ⅱ）求
的分布列和数学期望；
（Ⅲ）求在先后两次出现的点数中有5的条件下，方程
有实根的概率．
江西卷(理)
2005年
18．（本小题满分12分）
已知向量
.
是否存在实数
若存在，则求出x的值；若不存在，则证明之.
2006年
18．(本小题满分12分)
某商场举行抽奖促销活动，抽奖规则是：从装有9个白球、1个红球的箱子中每
次随机地摸出一个球，记下颜色后放回，摸出一个红球可获得奖金10元；摸出两个红
球可获得奖金50元．现有甲、乙两位顾客，规定：甲摸一次，乙摸两次．令ξ表示甲、
乙两人摸球后获得的奖金总额．求
(1)ξ的分布列； (2)ξ的数学期望．
2007年
18．（本小题满分12分）
如图，函数
的图象与轴交于点
，
且在该点处切线的斜率为
．
（1）求
和
的值；
（2）已知点
，点
是该函数图象上一点，
点
是
的中点，当
，
时，求
的值．
陕西卷(理)
2006年
（１８）（本小题满分１２分）
甲、乙、丙3人投篮，投进的概率分别是
（I）现3人各投篮1次，求3人都没有投进的概率；
（II）用表示投篮3次的进球数，求随机变量的概率分布及数学期望
2007年
18．（本小题满分12分）
某项选拔共有四轮考核，每轮设有一问题，能正确回答问题者进入下一轮考核，
否则即被淘汰．已知某选手能正确回答第一、二、三、四轮的问题的概率分别
为
且各轮问题能否正确回答互不影响．
（Ⅰ）求该选手被淘汰的概率；
（Ⅱ）该选手在选择中回答问题的个数记为，求随机变量的分布列与数学期望．
（注：本小题结果可用分数表示）
四川卷(理)
2006年
（18）（本大题满分12分）
某课程考核分理论与实验两部分进行，每部分考核成绩只记“合格”与
“不合格”，两部分考核都是“合格”则该课程考核“合格”，甲、乙、
丙三人在理论考核中合格的概率分别为
；在实验考核中合格的
概率分别为
，所有考核是否合格相互之间没有影响
（Ⅰ）求甲、乙、丙三人在理论考核中至少有两人合格的概率；
（Ⅱ）求这三人该课程考核都合格的概率。（结果保留三位小数）
2007年
（18）（本小题满分12分）厂家在产品出厂前，需对产品做检验，厂家将一批
产品发给商家时，商家按合同规定也需随机抽取一定数量的产品做检验，以决定
是否接收这批产品.
（Ⅰ）若厂家库房中的每件产品合格的概率为0.8，从中任意取出4件进行检验.
求至少有1件是合格品的概率;
（Ⅱ）若厂家发给商家20件产品，其中有3件不合格，按合同规定该商家从中任
取2件，都进行检验，只有2件都合格时才接收这批产品，否则拒收.求该商家可
能检验出不合格产品数的分布列及期望，并求该商家拒收这批产品的概率.
安徽卷(理)
2006年
（18）（本小题满分12分）
在添加剂的搭配适用中，为了找到最佳的搭配方案，需要对各种不同的搭配方式
作比较，在试制某种牙膏新品种时，需要选用两种不同的添加剂。现在芳香度分
别为0，1，2，3，4，5的六种添加剂可供选用。根据实验设计学原理，通常首先
要随机选取两种不同的添加剂进行搭配实验。用表示所选用的两种不同的添加剂
的芳香度之和。
（Ⅰ）写出
的分布列：（以列表的形式给出结论，不必写计算过程）
（Ⅱ）求的数学期望E
。（要求写出计算过程或说明道理）
2007年
17．（本小题满分14分）
如图，在六面体
中，四边形
是边长为
2的正方形，四边形
是边长为1的正方形，
平面
，
平面
，
．
（Ⅰ）求证：
与共面，
与
共面．
（Ⅱ）求证：平面
平面
；
（Ⅲ）求二面角
的大小（用反三角函数值表示）．
海南宁夏卷(理)
2007年
18．（本小题满分12分）
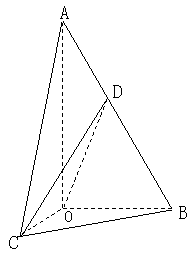
如图，在三棱锥
中，侧面
与侧面
均为等边三角形，
，
为中点．
（Ⅰ）证明：
平面；
（Ⅱ）求二面角
的余弦值．
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。
