福建(文)
三、解答题
(18)(本小题满分12分)
每次抛掷一枚骰子(六个面上分别标以数字![]()
(I)连续抛掷2次,求向上的数不同的概率;
(II)连续抛掷2次,求向上的数之和为6的概率;
(III)连续抛掷5次,求向上的数为奇数恰好出现3次的概率。
浙江(文)
三、解答题
(18)甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;
乙袋装有2个红球,n个白球.现从甲、乙两袋中各任取2个球.
(Ⅰ)若n=3,求取到的4个球全是红球的概率;
(Ⅱ)若取到的4个球中至少有2个红球的概率为![]() ,求n.
,求n.
天津(文)
三、解答题
(18)(本小题满分12分)
甲、乙两台机床相互没有影响地生产某种产品,甲机床产品的正品率
是0.9,乙机床产品的正品率是0.95.
(Ⅰ)从甲机床生产的产品中任取3件,求其中恰有2件正品的概率
(用数字作答);
(Ⅱ)从甲、乙两台机床生产的产品中各任取1件,求其中至少有1件
正品的概率(用数字作答).
江苏
一、选择题(每小题5分)
(3)某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.
已知这组数据的平均数为10,方差为2,则|x-y|的值为()
(A)1 (B)2 (C)3 (D)4
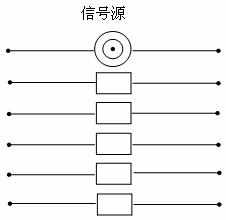
(10)下图中有一个信号源和五个接收器。接收器与信号源在同一个串联线
路中时,就能接收到信号,否则就不能接收到信号。若将图中左端的六个接
线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再
把所有六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到
信号的概率是()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
辽宁(文)
三、解答题
18.(本小题满分12分)
甲、乙两班各派2名同学参加年级数学竞赛,参赛同学成绩及格的概率都为0.6,
且参赛同学的成绩相互之间没有影响,求:
(1)甲、乙两班参赛同学中各有1名同学成绩及格的概率;
(2)甲、乙两班参赛同学中至少有1名同学成绩及格的概率.
重庆(文)
一、选择题(每小题5分)
(7)某地区有300家商店,其中大型商店有30家,中型商店有75家,
小型商店有195家,为了掌握各商店的营业情况,要从中抽取一个容
量为20的样本,若采用分层抽样的方法,抽取的中型商店数是()
(A)2 (B)3 (C)5 (D)13
解答
三、解答题
(17)(本小题满分13分)
甲、乙、丙三人在同一办公室工作,办公室里只有一部电话机,
设经该机打进的电话
是打给甲、乙、丙的概率依次为![]() 、
、![]() 、
、![]() .若在一段时间内打进
.若在一段时间内打进
三个电话,且各个电话相互独立.
求:
(Ⅰ)这三个电话是打给同一个人的概率;
(Ⅱ)这三个电话中恰有两个是打给甲的概率.
湖南(文)
三、解答题
17.(本小题满分12分)
某安全生产监督部门对5家小型煤矿进行安全检查(简称安检).若安检不合格,
则必须整改.若整改后经复查仍不合格,则强制关闭.设每家煤矿安检是否合格
是相互独立的,且每家煤矿整改前安检合格的概率是0.5,整改后安检合格的概率
是0.8,计算(结果精确到0.01):
(Ⅰ)恰好有两家煤矿必须整改的概率;
(Ⅱ)平均有多少家煤矿必须整改;
(Ⅲ)至少关闭一家煤矿的概率.
湖北(文)
二、填空题( 每题5分)
12.接种某疫苗后,出现发热反应的概率为0.80.现有5人接种该疫苗,至少
有3人出现发热反应的概率为_____________。(精确到0.01)
三、解答题
17.(本小题满分12分)
某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参
加了其中一组,在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人
占10%。登山组的职工占参加活动总人数的![]() ,且该组中,青年人占50%,中年人
,且该组中,青年人占50%,中年人
占40%,老年人占10%。为了了解各组不同年龄层次的职工对本次活动的满意程度,
现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本,试确定
(Ⅰ)游泳组中,青年人、中年人、老年人分别所占的比例;
(Ⅱ)游泳组中,青年人、中年人、老年人分别应抽取的人数。
广东
三、解答题
16.(本小题满分12分)
某运动员射击一次所得环数X的分布如下:
|
X |
0-6 |
7 |
8 |
9 |
10 |
|
p |
0 |
0.2 |
0.3 |
0.3 |
0.2 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为![]() 。
。
(Ⅰ)求该运动员两次都命中7环的概率:
(Ⅱ)求![]() 的分布列:
的分布列:
(Ⅲ)求![]() 的数学期望E
的数学期望E![]() 。
。
北京(文)
三、解答题
(18)(本小题共13分)
某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过:
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是0.5,0.6,0.9,
且三门课程考试是否及格相互之间没有影响.求:
(Ⅰ)该应聘者用方案一考试通过的概率;
(Ⅱ)该应聘者用方案二考试通过的概率.
上海(文)
一、填空题(每小题4分)
10.在一个小组中有8名女同学和4名男同学,从中任意地挑选2名同学担任
交通安全宣传志愿者,那么选到的两名都是女同学的概率是_________
(结果用分数表示)解答
山东(文)
三、解答题
(19)(本小题满分12分)
盒中装着标有数字1,2,3,4的卡片各2张,从盒中任意任取3张,
每张卡片被抽出的可能性都相等,求:
(Ⅰ)抽出的3张卡片上最大的数字是4的概率;
(Ⅱ)抽出的3张中有2张卡片上的数字是3的概率;
(Ⅲ)抽出的3张卡片上的数字互不相同的概率.
江西(文)
一、选择题(每题5分)
8.袋中有40个小球,其中红色球16个、蓝色球12个、白色球8个、黄色球4个,
从中随机抽取10个球作成一个样本,则这个样本恰好是按分层抽样方法得到
的概率为( )
A.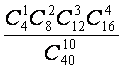 B.
B.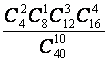 C.
C.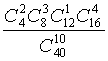 D.
D.
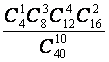
三、解答题
18.(本小题满分12分)
某商场举行抽奖促销活动,抽奖规则是:从装有9个白球、1个红球的箱子中
每次随机地摸出一个球,记下颜色后放回,摸出一个红球获得二等奖;摸出两个
红球获得一等奖.现有甲、乙两位顾客,规定:甲摸一次,乙摸两次.求
(1)甲、乙两人都没有中奖的概率;
(2)甲、乙两人中至少有一人获二等奖的概率.
陕西(文)
三、解答题
17.(本小题满分12分)
甲,乙,丙三人投篮,投进的概率分别是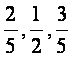 。现3人各投篮1次,求
。现3人各投篮1次,求
(Ⅰ)3人都投进的概率;
(Ⅱ)3人中恰有2人投进的概率。
安徽(文)
一、选择题(每题5分)
(12)在正方体上任选3个顶点连成三角形,则所得的三角形是直角非等腰三角形的
概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
三、 解答题
(18)(本大题满分12分)在添加剂的搭配使用中,为了找到最佳的搭配方案,
需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种
不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。
根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。
(Ⅰ)求所选用的两种不同的添加剂的芳香度之和等于4的概率;
(Ⅱ)求所选用的两种不同的添加剂的芳香度之和不小于3的概率;
四川(文)
一、选择题(每小题5分)
(12)从![]() 到
到![]() 这
这![]() 个数字中任取
个数字中任取![]() 个数字组成一个没有重复数字的三位数,
个数字组成一个没有重复数字的三位数,
这个数不能被![]() 整除的概率为()
整除的概率为()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
三、解答题
(19)(本大题满分12分)
某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与
“不合格”,两部分考核都是“合格”则该课程考核“合格”,甲、乙、
丙三人在理论考核中合格的概率分别为![]() ;在实验考核中合格的概
;在实验考核中合格的概
率分别为![]() ,所有考核是否合格相互之间没有影响
,所有考核是否合格相互之间没有影响
(Ⅰ)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(Ⅱ)求这三人该课程考核都合格的概率。(结果保留三位小数)
全国卷(Ⅰ)文
三、解答题
(19) (本小题满分12分)
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验,每个试验组由4只小
白鼠组成,其中2只服用A,另2只服用B,然后观察疗效,若在一个试验组中,服用A有
效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组.设每只小白鼠服用A
有效的概率为![]() ,服用B有效的概率为
,服用B有效的概率为![]() .
.
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,求这3个试验组中至少有一个甲类组的概率.
全国卷(Ⅱ)文
二、填空题(每小题4分)
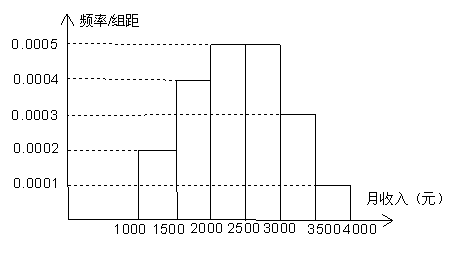
(16)一个社会调查机构就某地居民的月收入调查了10000人,并根据所得
数据画了样本的频率分布直方图(如下图)。为了分析居民的收入与年龄、
学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作
进一步调查,则在![]() (元)月收入段应抽出_____人。
(元)月收入段应抽出_____人。
三、解答题
(19)(本小题满分12分)
某批产品成箱包装,每箱5件,一用户在购进该批产品前先取出3箱,
再从每箱中任意抽取2件产品进行检验。设取出的第一、二、三箱中
分别有0件、1件、2件二等品,其余为一等品。
(I)求取6件产品中有1件产品是二等品的概率。
(II)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购
买这批产品,求这批产品被用户拒绝的概率。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。