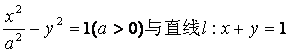 相交于两个不同的点A、B.
相交于两个不同的点A、B.解答题
全国卷Ⅰ(文)
2004年
22.(本小题满分14分)
设双曲线C: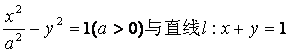 相交于两个不同的点A、B.
相交于两个不同的点A、B.
(I)求双曲线C的离心率e的取值范围:
(II)设直线l与y轴的交点为P,且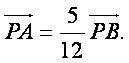 求a的值.
求a的值.
2005年
(22)(本大题满分14分)
已知椭圆的中心为坐标原点O,焦点在![]() 轴上,斜率为1且过椭圆右焦点F的
轴上,斜率为1且过椭圆右焦点F的
直线交椭圆于A、B两点,![]() 与
与![]() 共线
共线![]()
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且![]() ,
,
证明![]() 为定值
为定值![]()
2006年
(22)(本小题满分14分)
设a为实数,函数f(x)=x![]() -ax
-ax![]() +(a
+(a![]() -1)x在(-
-1)x在(-![]() ,0)和(1,+
,0)和(1,+![]() )都是增函数,
)都是增函数,
求a的取值范围.
2007年
(22)(本小题满分12分)
已知椭圆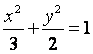 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 的直线交椭圆于B,D两点,
的直线交椭圆于B,D两点,
过![]() 的直线交椭圆于A,C两点,且
的直线交椭圆于A,C两点,且![]() ,垂足为P.
,垂足为P.
(Ⅰ)设P点的坐标为![]() ,证明:
,证明: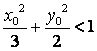 ;
;
(Ⅱ)求四边形ABCD的面积的最小值.
全国卷Ⅱ(文)
2004年
22.(本小题满分14分)
给定抛物线C:![]() F是C的焦点,过点F的直线
F是C的焦点,过点F的直线![]() 与C相交于A、B两点.
与C相交于A、B两点.
(Ⅰ)设![]() 的斜率为1,求
的斜率为1,求![]() 夹角的大小;
夹角的大小;
(Ⅱ)设![]() ,求
,求![]() 在
在![]() 轴上截距的变化范围.
轴上截距的变化范围.
2005年
(22)(本小题满分12分)
![]() 、
、![]() 、
、![]() 、
、![]() 四点都在椭圆
四点都在椭圆 上,
上,![]() 为椭圆在
为椭圆在![]() 轴正半轴上的焦点.
轴正半轴上的焦点.
已知![]() 与
与![]() 共线,
共线,![]() 与
与![]() 共线,且
共线,且![]() .求四边形
.求四边形![]() 的面积
的面积
的最小值和最大值.
2006年
(22)(本小题满分12分)
已知抛物线![]() 的焦点为F,A、B是抛物线上的两动点,且
的焦点为F,A、B是抛物线上的两动点,且![]()
过A、B两点分别作抛物线的切线,设其交点为M。
(I)证明![]() 为定值;
为定值;
(II)设![]() 的面积为S,写出
的面积为S,写出![]() 的表达式,并求S的最小值。
的表达式,并求S的最小值。
2007年
22.(本小题满分12分)
已知函数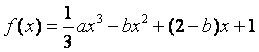
在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值,且
处取得极小值,且![]() .
.
(1)证明![]() ;
;
(2)若z=a+2b,求z的取值范围。
全国卷Ⅲ(文)
2004年
22.(本小题满分12分)设椭圆 的两个焦点是
的两个焦点是![]() 与
与![]() ,
,
且椭圆上存在一点![]() ,使得直线
,使得直线![]() 与
与![]() 垂直.
垂直.
(1)求实数![]() 的取值范围;
的取值范围;
(2)设![]() 是相应于焦点
是相应于焦点![]() 的准线,直线
的准线,直线![]() 与
与![]() 相交于点
相交于点![]() ,若
,若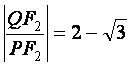 ,
,
求直线![]() 的方程.
的方程.
2005年
(22) (本小题满分14分)
设![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是AB的垂直平分线,
是AB的垂直平分线,
(Ⅰ)当且仅当![]() 取何值时,直线
取何值时,直线![]() 经过抛物线的焦点F?证明你的结论;
经过抛物线的焦点F?证明你的结论;
(Ⅱ)当![]() 时,求直线
时,求直线![]() 的方程
的方程![]()
全国卷Ⅳ(文)
2004年
22.(本小题满分14分)
双曲线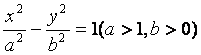 的焦距为2c,直线
的焦距为2c,直线![]() 过点(a,0)和(0,b),
过点(a,0)和(0,b),
且点(1,0)到直线![]() 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线![]() 的距离之和
的距离之和 求双
求双
曲线的离心率e的取值范围.
北京卷(文)
2004年
(20)(本小题满分12分)
给定有限个正数满足条件T:每个数都不大于50且总和L=1275。现将
这些数按下列要求进行分组, 每组数之和不大于150且分组的步骤是:
首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和
的差![]() 与所有可能的其他选择
相比是最小的,
与所有可能的其他选择
相比是最小的,![]() 称为第一组余差;
称为第一组余差;
然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构
成第二组,这时的余差为![]() ;
如此继续构成第三组(余差为
;
如此继续构成第三组(余差为![]() )、第四组
)、第四组
(余差为![]() )、……,直至第N组(余差为
)、……,直至第N组(余差为![]() )把这些数全部分
完为止。
)把这些数全部分
完为止。
(I)判断![]() 的大小关系,并指出除第N组外的每组至少含有几个数
的大小关系,并指出除第N组外的每组至少含有几个数
(II)当构成第n(n<N)组后,指出余下的每个数与![]() 的大小关系,并证明
的大小关系,并证明
![]()
(III)对任何满足条件T的有限个正数,证明:![]()
2005年
(20)(本小题共14分)
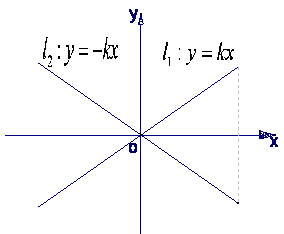 如图,直线
如图,直线![]() 与直线
与直线![]() 之间的阴影区域(不含边界)记为
之间的阴影区域(不含边界)记为![]() ,
,
其左半部分记为![]() ,右半部分记为
,右半部分记为![]()
![]()
(Ⅰ)分别有不等式组表示![]() 和
和![]()
![]()
(Ⅱ)若区域![]() 中的动点
中的动点![]() 到
到![]() 的距离
的距离
之积等于![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅲ)设不过原点![]() 的直线
的直线![]() 与(Ⅱ)中的曲线
与(Ⅱ)中的曲线![]()
相交于![]() 两点,且与
两点,且与![]() 分别交于
分别交于![]() 两点.
两点.
求证△![]() 的重心与△
的重心与△![]() 的重心重合
的重心重合![]()
2006年
(20)(本小题共14分)
设等差数列{an}的首项a1及公差d都为整数,前n项和为Sn.
(Ⅰ)若a11=0,S14=98,求数列{an}的通项公式;
(Ⅱ)若a1≥6,a11>0,S14≤77,求所有可能的数列{an}的通项公式.
2007年
20.(本小题共14分)
已知函数![]() 与
与![]() 的图象相交于
的图象相交于![]() ,
,![]() ,
,![]() ,
,![]() 分别
分别
是![]() 的图象在
的图象在![]() 两点的切线,
两点的切线,![]() 分别是
分别是![]() ,
,![]() 与
与![]() 轴的交点.
轴的交点.
(I)求![]() 的取值范围;
的取值范围;
(II)设![]() 为点
为点![]() 的横坐标,当
的横坐标,当![]() 时,写出
时,写出![]() 以
以![]() 为自变量的函数式,
为自变量的函数式,
并求其定义域和值域;
(III)试比较![]() 与
与![]() 的大小,并说明理由(
的大小,并说明理由(![]() 是坐标原点).
是坐标原点).
天津卷(文)
2004年
22.(本小题满分14分)
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点
,相应于焦点![]()
![]() 的
的
准线![]() 与
与![]() 轴相交于点A,
轴相交于点A,![]() ,过点A的直线与椭圆相交于P、Q两点。
,过点A的直线与椭圆相交于P、Q两点。
(1)求椭圆的方程及离心率;(2)若![]() ,求直线PQ的方程。
,求直线PQ的方程。
2005年
(22)(本小题满分14分)
抛物线C的方程为![]() ,过抛物线C上一点P(x0,y0)(x0¹0)作斜率
,过抛物线C上一点P(x0,y0)(x0¹0)作斜率
为k1,k2的两条直线分别交抛物线C于A(x1,y1)、B(x2,y2)两点(P、A、B三点
互不相同),且满足![]()
![]()
(Ⅰ)求抛物线C的焦点坐标和准线方程
(Ⅱ)设直线AB上一点M,满足![]() ,证明线段PM的中点在y轴上
,证明线段PM的中点在y轴上
(Ⅲ)当![]() =1时,若点P的坐标为(1,-1),求ÐPAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求ÐPAB为钝角时点A的纵坐标![]() 的取值范围
的取值范围
2006年
(22)(本小题满分14分)
如图,双曲线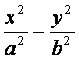 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为![]() ,F1、F2分别
,F1、F2分别
为左、右焦点,M为左准线与渐近线在第二象限内的交点,且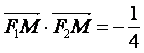 .
.
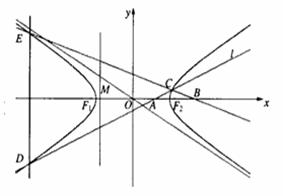
(Ⅰ)求双曲线的方程;
(Ⅱ)设A(m,0)和B(![]() ,0)
,0)![]()
是x轴上的两点.过点A作斜率不为0的
直线l,使得l交双曲线于C、D两点,
作直线BC交双曲线于另一点E.证明直线DE垂直于x轴.
2007年
(22)(本小题满分14分)
设椭圆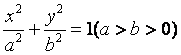 的左、右焦点分别为
的左、右焦点分别为![]() 是椭圆上的一点,
是椭圆上的一点,![]() ,
,
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)求![]() 使得下述命题成立:设圆
使得下述命题成立:设圆![]() 上任意点
上任意点![]() 处的切线交
处的切线交
椭圆于![]() ,
,![]() 两点,则
两点,则![]() .
.
上海卷(文)
2004年
22、(本题满分18分) 第1小题满分6分, 第2小题满分4分, 第3小题满分8分
设P1(x1,y1), P1(x2,y2),…, Pn(xn,yn)(n≥3,n∈N) 是二次曲线C上的点,
且a1=![]() 2,
a2=
2,
a2=![]() 2,
…, an=
2,
…, an=![]() 2构成了一个公差为d(d≠0)
的等差数列,
2构成了一个公差为d(d≠0)
的等差数列,
其中O是坐标原点. 记Sn=a1+a2+…+an.
(1)
若C的方程为![]() -y2=1,n=3.
点P1(3,0)
及S3=162,
求点P3的坐标;
-y2=1,n=3.
点P1(3,0)
及S3=162,
求点P3的坐标;
(只需写出一个)
(2) 若C的方程为y2=2px(p≠0). 点P1(0,0), 对于给定的自然数n, 证明:
(x1+p)2, (x2+p)2, …,(xn+p)2成等差数列;
(3)
若C的方程为![]() (a>b>0).
点P1(a,0),
对于给定的自然数n,
当
(a>b>0).
点P1(a,0),
对于给定的自然数n,
当
公差d变化时, 求Sn的最小值.
2005年
22.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,
第3小题满分6分![]()
对定义域是![]() .
.![]() 的函数
的函数![]() .
.![]() ,
,
规定:函数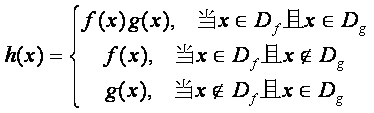
![]()
(1)若函数![]()
![]() ,
,![]() ,写出函数
,写出函数![]() 的解析式;
的解析式;
(2)求问题(1)中函数![]() 的值域;
的值域;
(3)若![]() ,其中
,其中![]() 是常数,且
是常数,且![]() ,请设计一个定义域为R的
,请设计一个定义域为R的
函数![]() ,及一个
,及一个![]() 的值,使得
的值,使得![]() ,并予以证明
,并予以证明![]()
2006年
22.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,
第3小题满分8分.
已知函数y=x+![]() 有如下性质,如果常数a>0,那么该函数在
有如下性质,如果常数a>0,那么该函数在![]() ]上是
]上是
减函数,在[![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)如果函数y=x+![]() 在(0,4]上是减函数,在[4,+∞)上是增函数,
在(0,4]上是减函数,在[4,+∞)上是增函数,
求实常数b的值;
(2)设常数c∈[1,4],求函数f(x)=x+![]() (1≤x≤2)的最大值和最小值;
(1≤x≤2)的最大值和最小值;
(3)当n是正整数时,研究函数g(x)=xn-![]() (c>0)的单调性,并说明理由.
(c>0)的单调性,并说明理由.
2007年
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分5分,
第3小题满分9分.
我们把由半椭圆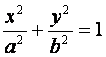
![]() 与半椭圆
与半椭圆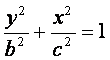
![]() 合成的曲线称作
合成的曲线称作
“果圆”,其中![]() ,
,![]() ,
,![]() .
.
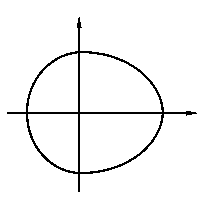 如图,设点
如图,设点![]() ,
,![]() ,
,![]() 是相应椭圆的焦点,
是相应椭圆的焦点,![]() ,
,![]() 和
和![]() ,
,![]() 是“果圆”
与
是“果圆”
与![]() ,
,![]() 轴的
轴的
交点,![]() 是线段
是线段![]() 的中点.
的中点.
(1)若![]() 是边长为1的等边三角形,求该
是边长为1的等边三角形,求该
“果圆”的方程;
(2)设![]() 是“果圆”的半椭圆
是“果圆”的半椭圆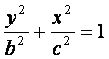
![]() 上任意一点.求证:当
上任意一点.求证:当![]() 取得最小值时,
取得最小值时,
![]() 在点
在点![]() 或
或![]() 处;
处;
(3)若![]() 是“果圆”上任意一点,求
是“果圆”上任意一点,求![]() 取得最小值时点
取得最小值时点![]() 的横坐标.
的横坐标.
辽宁卷(文)
2004年
22.(本小题满分12分)
已知函数![]() .
.
(1)求函数![]() 的反函数
的反函数![]() 的导数
的导数![]()
(2)假设对任意![]() 成立,求实
成立,求实
数m的取值范围.
2005年
22.(本小题满分12分)
函数![]() 在区间(0,+∞)内可导,导函数
在区间(0,+∞)内可导,导函数![]() 是减函数,且
是减函数,且![]() 设
设
![]() 是曲线
是曲线![]() 在点(
在点(![]() )得的切线方程,并设
)得的切线方程,并设
函数![]()
(Ⅰ)用![]() 、
、![]() 、
、![]() 表示m;
表示m;
(Ⅱ)证明:当![]() ;
;
(Ⅲ)若关于![]() 的不等式
的不等式 上恒成立,其中a、b为实数,
上恒成立,其中a、b为实数,
求b的取值范围及a与b所满足的关系.
2006年(文)
22.(本小题满分14分)
已知点![]() 是抛物线
是抛物线![]() 上的两个动点,
上的两个动点,![]() 是坐标原点,
是坐标原点,
向量![]() 满足
满足![]() ,设圆
,设圆![]() 的方程为
的方程为![]() .
.
(1)证明线段![]() 是圆
是圆![]() 的直径;
的直径;
(2)当圆![]() 的圆心到直线
的圆心到直线![]() 的距离的最小值为
的距离的最小值为 时,求
时,求![]() 的值.
的值.
2007年
22.(本小题满分12分)
已知函数![]() ,
,![]() ,且对任意的实数
,且对任意的实数![]() 均
均
有![]() ,
,![]() .
.
(I)求函数![]() 的解析式;
的解析式;
(II)若对任意的![]() ,恒有
,恒有![]() ,求
,求![]() 的取值范围.
的取值范围.
江苏卷
2004年
22.已知函数![]() 满足下列条件:对任意的实数x1,x2都有
满足下列条件:对任意的实数x1,x2都有
![]() 和
和![]() ,其中
,其中![]() 是大于0的常数.
是大于0的常数.
设实数a0,a,b满足
![]() 和
和![]()
(Ⅰ)证明![]() ,并且不存在
,并且不存在![]() ,使得
,使得![]() ;
;
(Ⅱ)证明![]() ;
;
(Ⅲ)证明![]() .
.
浙江卷(文)
2004年
(22)(本题满分14分)
解:已知双曲线的中心在原点,右顶点为A(1,0)点P、Q在双
曲线的右支上,支M(m,0)到直线AP的距离为1。
(Ⅰ)若直线AP的斜率为k,且 ,求实数m的
,求实数m的
取值范围;
(Ⅱ)当![]() 时,ΔAPQ的内心恰好是点M,求此双曲
时,ΔAPQ的内心恰好是点M,求此双曲
线的方程。
2005年
20.函数f(x)和g(x)的图象关于原点对称,且f(x)=x2=2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|.
(Ⅲ)若![]() 在
在![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围
的取值范围
2006年
(20)设f(x)=3ax2+2bx+c,若a+b+c=0,f(0)f(1)>0,求证:
(Ⅰ)方程f(x)=0有实根;
(Ⅱ)-2<![]() <-1;
<-1;
(Ⅲ)设x1,x2是方程f(x)=0的两个实根,则![]() ≤|x1-x2|<
≤|x1-x2|<![]() .
.
福建卷(文)
2004年
22.(本小题满分14分)
已知f(x)= 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)= 的两个非零实根为x1、x2.试问:
的两个非零实根为x1、x2.试问:
是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]
恒成立?若存在,求m的取值范围;若不存在,请说明理由.
2005年
22.(本小题满分12分)
已知方向向量为v=(1,![]() )的直线l过点(0,-2
)的直线l过点(0,-2![]() )和
)和
椭圆C: 的焦点,且椭圆C的中心关于直线l的对称点
的焦点,且椭圆C的中心关于直线l的对称点
在椭圆C的右准线上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在过点E(-2,0)的直线m交椭圆C于点M、N,
满足![]() cot∠MON≠0(O为原点).若存在,求直线m的方程;
cot∠MON≠0(O为原点).若存在,求直线m的方程;
若不存在,请说明理由.
2006年
(22)(本小题满分14分)
已知数列![]() 满足
满足![]()
(I)证明:数列![]() 是等比数列;
是等比数列;
(II)求数列![]() 的通项公式;
的通项公式;
(II)若数列![]() 满足
满足![]() 证明
证明![]() 是等差数列。
是等差数列。
2007年
22.(本小题满分14分)
如图,已知![]() ,直线
,直线![]() ,
,![]() 为平面上的动点,过点
为平面上的动点,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,
,
且![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() 两点,交直线
两点,交直线![]() 于点
于点![]() .
.
(1)已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的最小值.
的最小值.
湖北卷(文)
2004年
22.(本小题满分14分)
已知![]() 的图象相切.
的图象相切.
(Ⅰ)求b与c的关系式(用c表示b);
(Ⅱ)设函数![]() 内有极值点,求c的取值范围.
内有极值点,求c的取值范围.
2005年
22.(本小题满分14分)
设A、B是椭圆![]() 上的两点,点N(1,3)是线段AB的中点,
上的两点,点N(1,3)是线段AB的中点,
线段AB的垂直平分线与椭圆相交于C、D两点![]()
(Ⅰ)确定![]() 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的![]() ,使得A、B、C、D四点在同一个圆上?并说明理由
,使得A、B、C、D四点在同一个圆上?并说明理由![]()
2006年
21.(本小题满分14分)
设A、B分别为椭圆 =1(a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,
=1(a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,
且x=4是它的右准线。
(Ⅰ)求椭圆的方程;
(Ⅱ)设P为右准线上不同于点(4,0)的任意一点,若直线AB,BP分别与椭圆相交于
异于A,B的M、N,证明点B在以MN为直径的圆内.
2007年
21.(本小题满分14分)
在平面直角坐标系![]() 中,过定点
中,过定点![]() 作直线与抛物线
作直线与抛物线![]() (
(![]() )
)
相交于![]() 两点.
两点.
(I)若点![]() 是点
是点![]() 关于坐标原点
关于坐标原点![]() 的对称点,求
的对称点,求![]() 面积的最小值;
面积的最小值;
(II)是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的
为直径的圆截得的
弦长恒为定值?若存在,求出![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.

(此题不要求在答题卡上画图)
湖南卷(文)
2004年
22.(本小题满分14分)
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线
交于A,B两点,点Q是点P关于原点的对称点。
(I)设点P分有向线段![]() 所成的比为
所成的比为![]() ,证明:
,证明:![]()
![]()
(II)设直线AB的方程是x-2y+12=0,过A,B两点的圆C与抛物线在点A处有
共同的切线,求圆C的方程.
2005年
21.(本小题满分14分)
已知椭圆C:![]() +
+![]() =1(a>b>0)的左.右焦点为F1、F2,离心率为e.
=1(a>b>0)的左.右焦点为F1、F2,离心率为e.
直线l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公
共点,P是点F1关于直线l的对称点,设![]() =λ
=λ![]() .
.
(Ⅰ)证明:λ=1-e2;
(Ⅱ)若 ,△PF1F2的周长为6;写出椭圆C的方程;
,△PF1F2的周长为6;写出椭圆C的方程;
(Ⅱ)确定λ的值,使得△PF1F2是等腰三角形.
2006年
21.(本小题满分14分)
已知椭圆C1∶ =1,抛物线C2∶(y-m)2=2px(p>0),且C1、C2的公共弦AB
=1,抛物线C2∶(y-m)2=2px(p>0),且C1、C2的公共弦AB
过椭圆C1的右焦点.
(Ⅰ)当AB⊥x轴时,求p、m的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)若P=![]() 且抛物线C2的焦点在直线AB上,求m的值及AB的方程.
且抛物线C2的焦点在直线AB上,求m的值及AB的方程.
2007年
21.(本小题满分13分)
已知函数 在区间
在区间![]() ,
,![]() 内各有一个极值点.
内各有一个极值点.
(I)求![]() 的最大值;
的最大值;
(II)当![]() 时,设函数
时,设函数![]() 在点
在点![]() 处的切线为
处的切线为![]() ,若
,若![]() 在点
在点![]() 处穿过
处穿过
函数![]() 的图象(即动点在点
的图象(即动点在点![]() 附近沿曲线
附近沿曲线![]() 运动,经过点
运动,经过点![]() 时,从
时,从![]() 的一侧
的一侧
进入另一侧),求函数![]() 的表达式.
的表达式.
广东卷(文)
2004年
22.(14分)设直线![]() 与椭圆
与椭圆![]() 相交于A、B两点,
相交于A、B两点,![]() 又与双曲线x2–y2=1
又与双曲线x2–y2=1
相交于C、D两点,
C、D三等分线段AB. 求直线![]() 的方程.
的方程.
2005年
20.(本小题满分14分)
在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、
y轴的正半轴上,A点与坐标原点重合(如图5所示).将矩形折叠,使A点落
在线段DC上.
(Ⅰ)若折痕所在直线的斜率为k,
试写出折痕所在直线的方程;
(Ⅱ)求折痕的长的最大值.

2006年
20.(本小题满分12分)
A是由定义在[2,4]上且满足如下条件的函数![]() (x)组成的集合:
(x)组成的集合:
①对任意的![]() 都有
都有![]() (2x)
(2x)![]() ;②存在常数L(0<L<1),
;②存在常数L(0<L<1),
使得对任意的x1,x2![]() [1,2],都有|
[1,2],都有|![]() (2x1)-
(2x1)-![]() (2x2)|
(2x2)|![]() .
.
(Ⅰ)设![]() (x)=
(x)=![]() 证明:
证明:![]() (x)
(x)![]() A:
A:
(Ⅱ)设![]() (x)
(x)![]() ,如果存在x0
,如果存在x0![]() (1,2),使得x0=
(1,2),使得x0=![]() (2x0),
(2x0),
那么这样的x0是唯一的:
(Ⅲ)设![]()
![]() 任取x1
任取x1![]() (1,2),令xn+1=
(1,2),令xn+1=![]() (2xn),n=1,2……证明:给定
(2xn),n=1,2……证明:给定
正整数k,对任意的正整数p,成立不等式 。
。
2007年
21.(本小题满分14分)
已知![]() 是实数,函数
是实数,函数![]() ,如果函数
,如果函数![]() 在区间
在区间![]() 上有零点,求
上有零点,求![]() 的取值范围.
的取值范围.
重庆卷(文)
2004年
22.(本小题满分14分)
设数列![]() 满足:
满足:![]()
(1)
令![]() 求数列
求数列![]() 的通项公式;
的通项公式;
(2)
求数列![]() 的前n项和
的前n项和![]() 。
。
2005年
22.(本小题满分12分)
数列![]() 记
记
(Ⅰ)求b1、b2、b3、b4的值;
(Ⅱ)求数列![]() 的通项公式及数列
的通项公式及数列![]() 的前n项和
的前n项和![]()
2006年
(22)(本小题满分12分)
如图,对每个正整数n,An(xn,yn)是抛物线x2=4y上的点,
过焦点F的直线FA.交抛物线于另一点Bn(sn,tn).

2007年
22.(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
已知各项均为正数的数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,
,
且![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 满足
满足![]() ,并记
,并记![]() 为
为![]() 的前
的前![]() 项和,
项和,
求证:![]() .
.
山东卷(文)
2005年
(22)
(本小题满分14分)已知动圆过定点 ,且与直线
,且与直线![]() 相切,其中
相切,其中![]() .
.
(I)求动圆圆心![]() 的轨迹的方程;
的轨迹的方程;
(II)设A、B是轨迹![]() 上异于原点
上异于原点![]() 的两个不同点,直线
的两个不同点,直线![]() 和
和![]() 的倾斜角分别
的倾斜角分别
为![]() 和
和![]() ,当
,当![]() 变化且
变化且![]() 时,证明直线
时,证明直线![]() 恒过定点,并求出该定点的坐标
恒过定点,并求出该定点的坐标![]()
2006年
(22)(本小题满分14分)
已知数列{![]() }中,
}中, 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(Ⅰ)令![]()
(Ⅱ)求数列![]()
(Ⅲ)设![]()
![]()
![]() 的前n项和。是否存在实数
的前n项和。是否存在实数![]() ,使得
,使得
数列 为等差数列?若存在,试求出
为等差数列?若存在,试求出![]() ;若不存在,则说明理由。
;若不存在,则说明理由。
2007年
22.(本小题满分14分)
已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,椭圆
轴上,椭圆![]() 上的点到焦点距离
上的点到焦点距离
的最大值为3,最小值为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点(
两点(![]() 不是左右顶点),且以
不是左右顶点),且以![]()
为直径的图过椭圆![]() 的右顶点.求证:直线
的右顶点.求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
江西卷(文)
2005年
22.(本小题满分14分)
已知数列{an}的前n项和Sn满足Sn-Sn-2=3
求数列{an}的通项公式.
2006年
22.(本小题满分14分)
已知各项均为正数的数列{an}满足 =anan+1,n∈N*.
=anan+1,n∈N*.
(1)求数列{an}的通项公式;
(2)设Sn=a21+a22+…+a2n,Tn= ,求Sn+Tn,并确定最小正整数
,求Sn+Tn,并确定最小正整数
n,使Sn+Tn为整数.
2007年
22.(本小题满分14分)
设动点![]() 到点
到点![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,
,![]() ,
,
且存在常数![]() ,使得
,使得![]() .
.
 (1)证明:动点
(1)证明:动点![]() 的轨迹
的轨迹![]() 为双曲线,并求出
为双曲线,并求出![]() 的方程;
的方程;
(2)如图,过点![]() 的直线与双曲线
的直线与双曲线![]() 的右支交于
的右支交于![]() 两点.
两点.
问:是否存在![]() ,使
,使![]() 是以点
是以点![]() 为直角顶点的等腰
为直角顶点的等腰
直角三角形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
陕西卷(文)
2006年
22.(本小题满分12分)
设![]() (k≥0)
(k≥0)
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)若函数![]() 的极小值大于0,求k的取值范围.
的极小值大于0,求k的取值范围.
2007年
22.(本小题满分14分)
已知椭圆 的离心率为
的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
求![]() 面积的最大值.
面积的最大值.
四川卷(文)
2006年
(22)(本大题满分14分)
已知两定点![]() ,满足条件
,满足条件![]() 的点
的点![]() 的轨迹是
的轨迹是
曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点
两点
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)如果![]() ,且曲线
,且曲线![]() 上存在点
上存在点![]() ,使
,使![]() ,
,
求![]() 的值和
的值和![]() 的面积S.
的面积S.
2007年
(22)(本小题满分14分)
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴
的交点为(xn+1,u)(u,N +),其中为正实数.
(Ⅰ)用xx表示xn+1;
(Ⅱ)若a1=4,记an=lg ,证明数列{a1}成等比数列,
,证明数列{a1}成等比数列,
并求数列{xn}的通项公式;
(Ⅲ)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
安徽卷(文)
2006年
(22)(本大题满分14分)如图,F为双曲线C: 的右
的右
焦点。P为双曲线C右支上一点,且位于![]() 轴上方,M为左准线上一点,
轴上方,M为左准线上一点,![]() 为坐标
为坐标
原点。已知四边形![]() 为平行四边形,
为平行四边形,![]() 。
。
(Ⅰ)写出双曲线C的离心率![]() 与
与![]() 的关系式;
的关系式;
(Ⅱ)当![]() 时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
时,经过焦点F且平行于OP的直线交双曲线于A、B点,若![]() ,
,
求此时的双曲线方程。

2007年
21.(本小题满分14分)
某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为![]() ,
,
以后每年交纳的数目均比上一年增加![]() ,因此,历年所交纳的储备金数目
,因此,历年所交纳的储备金数目
![]() 是一个公差为
是一个公差为![]() 的等差数列.与此同时,国家给予优惠的计息政策,不
的等差数列.与此同时,国家给予优惠的计息政策,不
仅采用固定利率,而且计算复利.这就是说,如果固定年利率为![]() ,那么,
,那么,
在第![]() 年末,第一年所交纳的储备金就变为
年末,第一年所交纳的储备金就变为![]() ,第二年所交纳的储备金就
,第二年所交纳的储备金就
变为![]() ,
,![]() .以
.以![]() 表示到第
表示到第![]() 年末所累计的储备金总额.
年末所累计的储备金总额.
(Ⅰ)写出![]() 与
与![]() 的递推关系式;
的递推关系式;
(Ⅱ)求证:![]() ,其中
,其中![]() 是一个等比数列,
是一个等比数列,![]() 是一个等差数列.
是一个等差数列.
海南宁夏卷(文)
2007年
 22.请考生在A、B两题中选一题作答,如果多做,则按所做的第一题记分.
22.请考生在A、B两题中选一题作答,如果多做,则按所做的第一题记分.
作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.
22.A(本小题满分10分)选修4-1:几何证明选讲
如图,已知![]() 是
是![]() 的切线,
的切线,![]() 为切点,
为切点,![]() 是
是![]() 的割线,与
的割线,与![]() 交于
交于![]() 两点,
两点,
圆心![]() 在
在![]() 的内部,点
的内部,点![]() 是
是![]() 的中点.
的中点.
(Ⅰ)证明![]() 四点共圆;
四点共圆;
(Ⅱ)求![]() 的大小.
的大小.
22.B(本小题满分10分)选修4-4:坐标系与参数方程
![]() 和
和![]() 的极坐标方程分别为
的极坐标方程分别为![]() .
.
(Ⅰ)把![]() 和
和![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)求经过![]() ,
,![]() 交点的直线的直角坐标方程.
交点的直线的直角坐标方程.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。