三、解答题
22.(本小题满分14分)
设动点![]() 到点
到点![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,
,![]() ,
,
且存在常数![]() ,使得
,使得![]() .
.
 (1)证明:动点
(1)证明:动点![]() 的轨迹
的轨迹![]() 为双曲线,并求出
为双曲线,并求出![]() 的方程;
的方程;
(2)如图,过点![]() 的直线与双曲线
的直线与双曲线![]() 的右支交于
的右支交于![]() 两点.
两点.
问:是否存在![]() ,使
,使![]() 是以点
是以点![]() 为直角顶点的等腰
为直角顶点的等腰
直角三角形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
解:(1)在![]() 中,
中,![]()
![]()
![]()
![]() (小于
(小于![]() 的常数)
的常数)
故动点![]() 的轨迹
的轨迹![]() 是以
是以![]() ,
,![]() 为焦点,实轴长
为焦点,实轴长![]() 的双曲线.
的双曲线.
方程为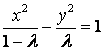 .
.
(2)方法一:在![]() 中,设
中,设![]() ,
,![]() ,
,![]() ,
,![]() .
.
假设![]() 为等腰直角三角形,则
为等腰直角三角形,则
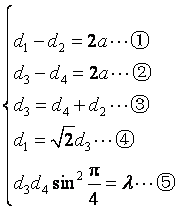
由②与③得![]() ,
,
则
由⑤得![]() ,
,
![]()
![]() ,
,
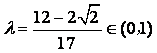
故存在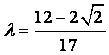 满足题设条件.
满足题设条件.
方法二:(1)设![]() 为等腰直角三角形,依题设可得
为等腰直角三角形,依题设可得

所以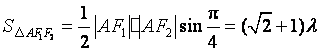 ,
, .
.
则![]() .①
.①
由 ,可设
,可设![]() ,
,
则![]() ,
,![]() .
.
则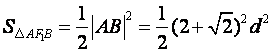 .②
.②
由①②得![]() .③
.③
根据双曲线定义![]() 可得,
可得,![]() .
.
平方得:![]() .④
.④
由③④消去![]() 可解得,
可解得,![]()
故存在![]() 满足题设条件.
满足题设条件.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。