 的左、右焦点分别为
的左、右焦点分别为三、解答题
(22)(本小题满分14分)
设椭圆 的左、右焦点分别为
的左、右焦点分别为![]() 是椭圆上的一点,
是椭圆上的一点,![]() ,
,
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)求![]() 使得下述命题成立:设圆
使得下述命题成立:设圆![]() 上任意点
上任意点![]() 处的切线交
处的切线交
椭圆于![]() ,
,![]() 两点,则
两点,则![]() .
.
本小题主要考查椭圆的标准方程和几何性质、直线方程、两条直线垂直、圆的方程
等基础知识,考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力.
满分14分.
(Ⅰ)证法一:由题设![]() 及
及![]() ,
,![]() ,不妨设点
,不妨设点![]() ,其中
,其中
![]() ,由于点
,由于点![]() 在椭圆上,有
在椭圆上,有 ,
,![]() ,
,
解得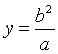 ,从而得到
,从而得到 ,
,
直线![]() 的方程为
的方程为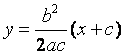 ,整理得
,整理得![]() .
.
由题设,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,即
,即 ,
,
将![]() 代入原式并化简得
代入原式并化简得![]() ,即
,即![]() .
.
证法二:同证法一,得到点![]() 的坐标为
的坐标为 ,
,
 过点
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,易知
,易知![]() ,故
,故

由椭圆定义得![]() ,又
,又![]() ,所以
,所以
 ,
,
解得 ,而
,而 ,得
,得 ,即
,即![]() .
.
(Ⅱ)解法一:圆![]() 上的任意点
上的任意点![]() 处的切线方程为
处的切线方程为![]() .
.
当![]() 时,圆
时,圆![]() 上的任意点都在椭圆内,故此圆在点
上的任意点都在椭圆内,故此圆在点![]() 处的切线必
处的切线必
交椭圆于两个不同的点![]() 和
和![]() ,因此点
,因此点![]() ,
,![]() 的坐标是方程组
的坐标是方程组
 的解.当
的解.当![]() 时,由①式得
时,由①式得

代入②式,得 ,即
,即
![]() ,
,
于是 ,
,
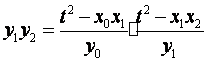

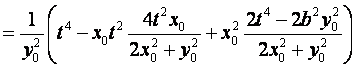
 .
.
若![]() ,则
,则
 .
.
所以,![]() .由
.由![]() ,得
,得![]() .
.
在区间![]() 内此方程的解为
内此方程的解为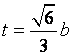 .
.
当![]() 时,必有
时,必有![]() ,同理求得在区间
,同理求得在区间![]() 内的解为
内的解为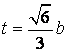 .
.
另一方面,当 时,可推出
时,可推出![]() ,从而
,从而![]() .
.
综上所述,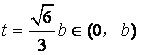 使得所述命题成立.
使得所述命题成立.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。