22．请考生在Ａ、Ｂ两题中选一题作答，如果多做，则按所做的第一题记分．

作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．

22．Ａ（本小题满分10分）选修4－1：几何证明选讲

如图，已知是的切线，为切点，是的割线，与交于两点，

圆心在的内部，点是的中点．

（Ⅰ）证明四点共圆；

（Ⅱ）求的大小．

22．Ｂ（本小题满分10分）选修4－4：坐标系与参数方程

和的极坐标方程分别为．

（Ⅰ）把和的极坐标方程化为直角坐标方程；

（Ⅱ）求经过，交点的直线的直角坐标方程．

22．Ａ

（Ⅰ）证明：连结．

因为与相切于点，所以．

因为是的弦的中点，所以．

于是．

由圆心在的内部，可知四边形的对角互补，所以四点共圆．

（Ⅱ）解：由（Ⅰ）得四点共圆，所以．

由（Ⅰ）得．

由圆心在的内部，可知．

所以．

22．Ｂ

解：以有点为原点，极轴为轴正半轴，建立平面直角坐标系，

两坐标系中取相同的长度单位．

（Ⅰ），，由得．

所以．

即为的直角坐标方程．

同理为的直角坐标方程．

（Ⅱ）由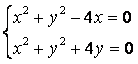

解得．

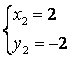即，交于点和．过交点的直线的直角坐标方程为．