解答题
全国卷Ⅰ(文)
2004年
17.(本小题满分12分)
等差数列{![]() }的前n项和记为Sn.已知
}的前n项和记为Sn.已知![]()
(Ⅰ)求通项![]() ;
;
(Ⅱ)若Sn=242,求n.
2005年
(17)(本大题满分12分)
设函数![]() 图像的一条对称轴是直线
图像的一条对称轴是直线![]()
![]()
(Ⅰ)求![]() ;
;
(Ⅱ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅲ)画出函数![]() 在区间
在区间![]() 上的图像
上的图像![]()

2006年
(17)(本小题满分12分)
已知{a![]() }为等比数列,a
}为等比数列,a![]() =2,a
=2,a![]() +a
+a![]() =
=![]() .求{a
.求{a![]() }的通项公式.
}的通项公式.
2007年
(17)(本小题满分10分)
设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,![]() .
.
(Ⅰ)求B的大小;
(Ⅱ)若![]() ,
,![]() ,求b.
,求b.
全国卷Ⅱ(文)
2004年
17.(本小题满分12分)
已知等差数列{![]() },
},![]()
(Ⅰ)求{![]() }的通项公式;
}的通项公式;
(Ⅱ)令![]() ,求数列
,求数列![]() 的前n项和Sn.
的前n项和Sn.
2005年
(17)(本小题满分12分)
已知![]() 为第二象限的角,
为第二象限的角,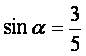 ,
,![]() 为第一象限的角,
为第一象限的角,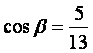 .求
.求![]() 的值.
的值.
2006年
(17)(本小题满分12分)
在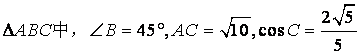 ,求
,求
(1)![]()
(2)若点![]()
2007年
17.(本小题满分10分)
设等比数列![]() 的公比
的公比![]() ,前
,前![]() 项和为
项和为![]() .已知
.已知![]() ,求
,求![]() 的通项公式.
的通项公式.
全国卷Ⅲ(文)
2004年
17.(本小题满分12分)
解方程![]()
2005年
(17)(本小题满分12分)
已知函数![]() 求使
求使![]() 为正值的
为正值的![]() 的集合
的集合![]()
全国卷Ⅳ(文)
2004年
17.(本小题满分12分)
已知α为第二象限角,且
sinα=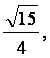 求
求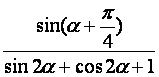 的值.
的值.
北京卷(文)
2004年
(15)(本小题满分14分)
在![]() 中,
中,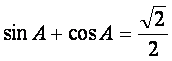 ,
,![]() ,
,![]() ,求
,求![]() 的值和
的值和![]() 的面积
的面积
2005年
(15)已知tan![]() =2,
=2,
求(1)tan(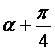 )的值
)的值
(2)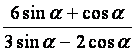 的值
的值
2006年
(15)(本小题共12分)
已知函数f(x)=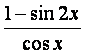 .
.
(Ⅰ)求f(x)的定义域;
(Ⅱ)设α是第四象限的角,且tanα=
-![]() ,求f(α)的值.
,求f(α)的值.
2007年
15.(本小题共12分)
记关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,不等式
,不等式![]() 的解集为
的解集为![]() .
.
(I)若![]() ,求
,求![]() ;
;
(II)若![]() ,求正数
,求正数![]() 的取值范围.
的取值范围.
天津卷(文)
2004年
17.(本小题满分12分)
已知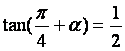
(1)求![]() 的值;(2)求
的值;(2)求 的值。
的值。
2005年
(17)(本小题满分12分)
已知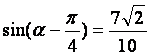 ,
,![]() ,求sina及
,求sina及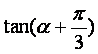
![]()
2006年
(17)(本小题满分12分)
已知tanα+cotα=![]() ,α∈(
,α∈(![]() ,
,![]() ),求cos2α和sin(2α+
),求cos2α和sin(2α+![]() )的值.
)的值.
2007年
(17)(本小题满分12分)
在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求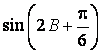 的值.
的值.
上海卷(文)
2004年
17、(本题满分12分)
已知复数z1满足(1+i)z1=-1+5i, z2=a-2-i, 其中i为虚数单位,
a∈R,
若![]() <
<![]() ,求a的取值范围.
,求a的取值范围.
2005年
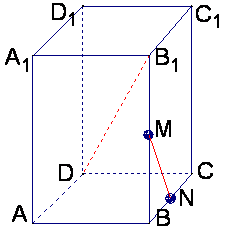
17.(本题满分12分)已知长方体![]() 中,M.N分别是
中,M.N分别是![]() 和BC的中点,
和BC的中点,
AB=4,AD=2,![]() 与平面ABCD所成角的大小为
与平面ABCD所成角的大小为![]() ,求异面直线
,求异面直线![]() 与MN所成角
与MN所成角
的大小![]() (结果用反三角函数值表示)
(结果用反三角函数值表示)
2006年
(17)(本题满分12分)
已知α是第一象限的角,且cosα=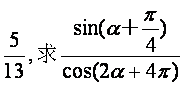 的值.
的值.
2007年
16.(本题满分12分)
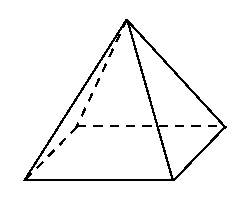 在正四棱锥
在正四棱锥![]() 中,
中,![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求
正四棱锥![]() 的体积
的体积![]() .
.
辽宁卷(文)
2004年
17.(本小题满分12分)
已知四棱锥P—ABCD,底面ABCD是菱形,![]() 平面ABCD,PD=AD,
平面ABCD,PD=AD,
点E为AB中点,点F为PD中点.
(1)证明平面PED⊥平面PAB;
(2)求二面角P—AB—F的平面角的余弦值.
2005年
17.(本小题满分12分)
已知三棱锥P—ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
(Ⅰ)证明PC⊥平面PAB;
(Ⅱ)求二面角P—AB—C的平面角的余弦值;
(Ⅲ)若点P、A、B、C在一个表面积为12π的
球面上,求△ABC的边长.
2006年(文)
(17) (本小题满分12分)
已知函数![]() ,
,![]() .求:
.求:
(I)
函数![]() 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量![]() 的集合;
的集合;
(II)
函数![]() 的单调增区间.
的单调增区间.
2007年
17.(本小题满分12分)
某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命
(单位:小时)进行了统计,统计结果如下表所示:
|
分组 |
[500,900) |
[900,1100) |
[1100,1300) |
[1300,1500) |
[1500,1700) |
[1700,1900) |
[1900, |
|
频数 |
48 |
121 |
208 |
223 |
193 |
165 |
42 |
|
频率 |
|
|
|
|
|
|
|
(I)将各组的频率填入表中;
(II)根据上述统计结果,计算灯管使用寿命不足1500小时的频率;
(III)该公司某办公室新安装了这种型号的灯管3支,若将上述频率作为概率,
试求至少有2支灯管的使用寿命不足1500小时的概率.
江苏卷
2004年
17.已知0<α<![]() ,tan
,tan![]() +cot
+cot![]() =
=![]() ,求sin(
,求sin(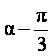 )的值.
)的值.
2005年
19.(本小题满分12分)如图,圆![]() 与圆
与圆![]() 的半径都是1,
的半径都是1,![]() ,
,
过动点P分别作圆![]() .圆
.圆![]() 的切线PM、PN(M.N分别为切点),使得
的切线PM、PN(M.N分别为切点),使得![]()
![]()
试建立适当的坐标系,并求动点P的轨迹方程![]()
2006年
(17)(本小题满分12分,第一小问满分5分,第二小问满分7分)
已知三点P(5,2)、![]() (-6,0)、
(-6,0)、![]() (6,0).
(6,0).
(Ⅰ)求以![]() 、
、![]() 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点P、![]() 、
、![]() 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为![]() 、
、![]() 、
、![]() ,
,
求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的双曲线的标准方程。
的双曲线的标准方程。
17.(本题满分12分)
某气象站天气预报的准确率为![]() ,计算(结果保留到小数点后第2位):
,计算(结果保留到小数点后第2位):
(1)5次预报中恰有2次准确的概率;(4分)
(2)5次预报中至少有2次准确的概率;(4分)
(3)5次预报中恰有2次准确,且其中第3次预报准确的概率.(4分)
浙江卷(文)
2004年
(17)(本题满分12分)
已知数列![]() 的前n项和为
的前n项和为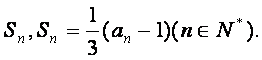
(Ⅰ)求![]() ;
;
(Ⅱ)求证数列![]() 是等比数列。
是等比数列。
2005年
15.已知函数![]()
(Ⅰ) 求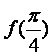 的值;
的值;
(Ⅱ) 设![]() ∈(0,
∈(0,![]() ),
),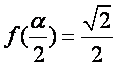 ,求sin
,求sin![]() 的值.
的值.
2006年
(15)若Sn是公差不为0的等差数列{an}的前n项和,且S1,S2,S4成等比数列.
(Ⅰ)求数列S1,S2,S4的公比;
(Ⅱ)若S2=4,求{an}的通项公式.
2007年
18.(本题14分)已知![]() 的周长为
的周长为![]() ,且
,且![]() .
.
(I)求边![]() 的长;
的长;
(II)若![]() 的面积为
的面积为 ,求角
,求角![]() 的度数.
的度数.
福建卷(文)
2004年
17.(本小题满分12分)
设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx,![]() sin2x),x∈R.
sin2x),x∈R.
(Ⅰ)若f(x)=1-![]() 且x∈[-
且x∈[-![]() ,
,![]() ],求x;
],求x;
(Ⅱ)若函数y=2sin2x的图象按向量c=(m,n)(|m|<![]() )平移后得到函数
)平移后得到函数
y=f(x)的图象,求实数m、n的值.
2005年
17.(本小题满分12分)
已知![]() .
.
(I)求sinx-cosx的值;
(Ⅱ)求![]() 的值.
的值.
2006年
(17)(本小题满分12分)
已知函数![]() =sin
=sin![]() x+
x+![]() sinxcosx,x∈R
sinxcosx,x∈R
(I)求函数![]() 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(II)函数![]() 的图象可以由函数
的图象可以由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
2007年
17.(本小题满分12分)
在![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)若![]() 边的长为
边的长为![]() ,求
,求![]() 边的长.
边的长.
湖北卷(文)
2004年
17.(本小题满分12分)
已知 的值.
的值.
2005年
17.(本小题满分12分)
已知向量a=(![]() ,x+1),b=
(1-x,t)
,x+1),b=
(1-x,t)![]() 若函数
若函数![]() =a·b在区间(-1,1)上
=a·b在区间(-1,1)上
是增函数,求t的取值范围![]()
2006年
16.(本小题满分12分)
设向量a=(sinx,cos x),b=(cosx,cosx),x∈R,函数f(x)=a(a+b)。
(Ⅰ)求函数f(x)的最大值与最小正周期;
(Ⅱ)求使不等式f(x)≥![]() 成立的x的取值集合。
成立的x的取值集合。
2007年
16.(本小题满分12分)
已知函数 ,
, .
.
(I)求![]() 的最大值和最小值;
的最大值和最小值;
(II)若不等式![]() 在
在 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
湖南卷(文)
2004年
17.(本小题满分12分)

2005年
16.(本小题满分12分)
已知数列![]() 为等差数列,且
为等差数列,且![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)证明
2006年
16.(本小题满分12分)
已知 ·cosθ=1,θ∈(0,π),求θ的值.
·cosθ=1,θ∈(0,π),求θ的值.
2007年
16.(本小题满分12分)
已知函数 .求:
.求:
(I)函数![]() 的最小正周期;
的最小正周期;
(II)函数![]() 的单调增区间.
的单调增区间.
广东卷(文)
2004年
17. (12分)已知![]() 成公比为2的等比数列(
成公比为2的等比数列(![]()
也成等比数列.
求![]() 的值.
的值.
2005年
15.(本小题满分12分)
化简
并求函数![]() 的值域和最小正周期.
的值域和最小正周期.
2006年
15.(本小题满分14分)
已知函数![]()
(Ⅰ)求f(x)的最小正周期:![]()
(Ⅱ)求f(x)的最大值和最小值:
(Ⅲ)若![]() 求sin2
求sin2![]() 的值。
的值。
2007年
16.(本小题满分14分)
已知![]() 三个顶点的直角坐标分别为
三个顶点的直角坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
重庆卷(文)
2004年
17.(本小题满分12分)
求函数![]() 的取小正周期和取小值;
的取小正周期和取小值;
并写出该函数在![]() 上的单调递增区间。
上的单调递增区间。
2005年
17.(本小题满分13分)
若函数 的最大值为
的最大值为![]() ,试确定常数a
,试确定常数a
的值.
2006年
(17)(本小题满分13分)
甲、乙、丙三人在同一办公室工作,办公室里只有一部电话机,
设经该机打进的电话
是打给甲、乙、丙的概率依次为![]() 、
、![]() 、
、![]() .若在一段时间内打进
.若在一段时间内打进
三个电话,且各个电话相互独立.
求:
(Ⅰ)这三个电话是打给同一个人的概率;
(Ⅱ)这三个电话中恰有两个是打给甲的概率.
2007年
17.(本小题满分13分.(Ⅰ)小问5分.(Ⅱ)小问8分.)
设甲、乙两人每次射击命中目标的概率分别为![]() 和
和![]() ,且各次射击相互独立.
,且各次射击相互独立.
(Ⅰ)若甲、乙各射击一次,求甲命中但乙未命中目标的概率;
(Ⅱ)若甲、乙各射击两次,求两人命中目标的次数相等的概率.
山东卷(文)
2005年
(17)(本小题满分12分)
已知向量![]() 和
和![]() ,
,
且 ,求
,求 的值
的值![]()
2006年
(17)(本小题满分12分)
设函数f(x)=![]()
(Ⅰ)求f(x)的单调区间;
(Ⅱ) 讨论f(x)的极值.
2007年
17.(本小题满分12分)
在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() .
.
(1)求![]() ;
;
(2)若![]() ,且
,且![]() ,求
,求![]() .
.
江西卷(文)
2005年
17.(本小题满分12分)
已知函数 (a,b为常数)且方程f(x)-x+12=0有两个实根
(a,b为常数)且方程f(x)-x+12=0有两个实根
为x1=3, x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;
2006年
17.(本小题满分12分)
已知函数f(x)=x3+ax2+bx+c在x=-![]() 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
2007年
17.(本小题满分12分)
已知函数 满足
满足 .
.
(1)求常数![]() 的值;
的值;
(2)解不等式 .
.
陕西卷(文)
2006年
17.(本小题满分12分)
甲,乙,丙三人投篮,投进的概率分别是 。现3人各投篮1次,求
。现3人各投篮1次,求
(Ⅰ)3人都投进的概率;
(Ⅱ)3人中恰有2人投进的概率。
2007年
17.(本小题满分12分)
设函数![]() ,其中向量
,其中向量![]() ,
,![]() ,
,![]() ,且
,且 .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)求函数![]() 的最小值.
的最小值.
四川卷(文)
2006年
(17)(本大题满分12分)
数列![]() 的前
的前![]() 项和记为
项和记为![]()
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)等差数列![]() 的各项为正,其前
的各项为正,其前![]() 项和为
项和为![]() ,且
,且![]() ,
,
又![]() 成等比数列,求
成等比数列,求![]()
2007年
(17)(本小题满分12分)
厂家在产品出厂前,需对产品做检验,厂家对一般产品致冷商家的,商家符合
规定拾取一定数量的产品做检验,以决定是否验收这些产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.3,从中任意取出4种进行检验,
求至少要1件是合格产品的概率.
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,
来进行检验,只有2件产品合格时才接收这些产品,否则拒收,分别求出该商家计算
出不合格产品为1件和2件的概率,并求该商家拒收这些产品的概率。
安徽卷(文)
2006年
(17)(本大题满分12分)已知
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值。
的值。
2007年
16.(本小题满分10分)
解不等式![]() .
.
海南宁夏卷(文)
2007年
17.(本小题满分12分)
如图,测量河对岸的塔高![]() 时,可以选与塔底
时,可以选与塔底![]() 在同一水平面内的两个侧点
在同一水平面内的两个侧点![]() 与
与![]() .
.
现测得![]() ,并在点
,并在点![]() 测得塔顶
测得塔顶![]() 的仰角为
的仰角为![]() ,求塔高
,求塔高![]() .
.

本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。