解答题

17．（本小题满分12分）

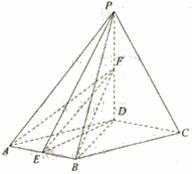
已知四棱锥P—ABCD，底面ABCD是菱形，平面ABCD，PD=AD，　

点E为AB中点，点F为PD中点.

   （1）证明平面PED⊥平面PAB；

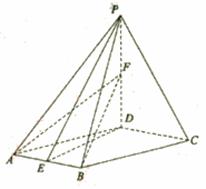
   （2）求二面角P—AB—F的平面角的余弦值.

本小题主要考查空间中的线面关系，四棱锥的有关概念及余弦定理等基础知识，

考查空间想象能力和推理能力. 满分12分.

   （1）证明：连接BD.

为等边三角形.

是AB中点，…………2分

面ABCD，AB面ABCD，

面PED，PD面PED，面PED.…………4分

面PAB，面PAB. ……………………6分

（2）解：平面PED，PE面PED，

连接EF，PED，

为二面角P—AB—F的平面角.  ………… 9分

设AD=2，那么PF=FD=1，DE=.

在

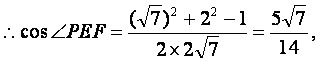
即二面角P—AB—F的平面角的余弦值为…12分