福建(文)
一、选择题(每小题5分)
7.已知![]() 是R上的减函数,则满足
是R上的减函数,则满足![]() 的实数x的取值范围是(
)
的实数x的取值范围是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知对任意实数![]() ,有
,有![]() ,
,![]() ,且
,且![]() 时,
时,![]() ,
,
![]() ,则
,则![]() 时( )
时( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
三、解答题
20.(本小题满分12分)
设函数![]() .
.
(Ⅰ)求![]() 的最小值
的最小值![]() ;
;
(Ⅱ)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
浙江(文)
二、填空题(每小题4分)
11.函数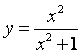 (
(![]() )的值域是
.
)的值域是
.
三、解答题
22.(本题15分)已知![]() .
.
(I)若![]() ,求方程
,求方程![]() 的解;
的解;
(II)若关于![]() 的方程
的方程![]() 在
在![]() 上有两个解
上有两个解![]() ,求
,求![]() 的取值范围,
的取值范围,
并证明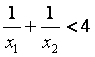 .
.
天津(文)
一、选择题(每小题5分)
(5)函数![]() 的反函数是(
)
的反函数是(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(10)设![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时,![]() ,若对任意的
,若对任意的![]() ,
,
不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是(
)
的取值范围是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
三、解答题
(21)(本小题满分14分)
设函数![]() (
(![]() ),其中
),其中![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 的极大值和极小值;
的极大值和极小值;
(Ⅲ)当![]() 时,证明存在
时,证明存在![]() ,使得不等式
,使得不等式![]() 对
对
任意的![]() 恒成立.
恒成立.
辽宁(文)
一、选择题(每小题5分)
2.若函数![]() 的反函数图象过点
的反函数图象过点![]() ,则函数
,则函数![]() 的图象必过点(
)
的图象必过点(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若函数![]() 的图象按向量
的图象按向量![]() 平移后,得到函数
平移后,得到函数![]() 的图象,则向量
的图象,则向量![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数![]() 的单调增区间为(
)
的单调增区间为(
)
A.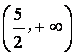 B.
B.![]() C.
C.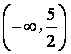 D.
D.![]()
二、填空题(每小题4分)
13.已知函数![]() 为奇函数,若
为奇函数,若![]() ,则
,则![]() .
.
三、解答题
22.(本小题满分12分)
已知函数![]() ,
,![]() ,且对任意的实数
,且对任意的实数![]() 均
均
有![]() ,
,![]() .
.
(I)求函数![]() 的解析式;
的解析式;
(II)若对任意的![]() ,恒有
,恒有![]() ,求
,求![]() 的取值范围.
的取值范围.
重庆(文)
一、选择题(每小题5分)
10.设![]() 为二次函数
为二次函数![]() 的图象与其反函数
的图象与其反函数![]() 的图象的
的图象的
一个交点,则( )
A.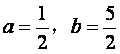 B.
B.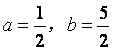
C.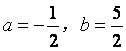 D.
D.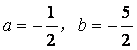
二、填空题(每小题4分)
16.函数![]() 的最小值为
.
的最小值为
.
三、解答题
20.(本小题满分12分)
用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为![]() ,
,
问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
湖南(文)
一、选择题(每小题5分)
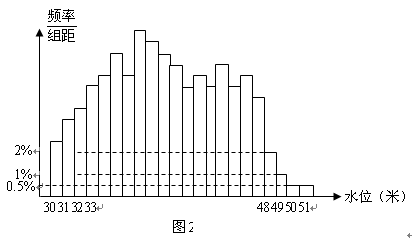
7.根据某水文观测点的历史统计数据,得到某条河流水位的频率分布直方图
(如图2).从图中可以看出,该水文观测点平均至少一百年才遇到一次的洪
水的最低水位是( )
A.48米 B.49米 C.50米 D.51米
8、函数 的图象和函数
的图象和函数![]() 的图象的交点个数是(
)
的图象的交点个数是(
)
A.4 B.3 C.2 D.1
三、解答题
21.(本小题满分13分)
已知函数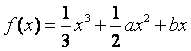 在区间
在区间![]() ,
,![]() 内各有一个极值点.
内各有一个极值点.
(I)求![]() 的最大值;
的最大值;
(II)当![]() 时,设函数
时,设函数![]() 在点
在点![]() 处的切线为
处的切线为![]() ,若
,若![]() 在点
在点![]() 处穿过
处穿过
函数![]() 的图象(即动点在点
的图象(即动点在点![]() 附近沿曲线
附近沿曲线![]() 运动,经过点
运动,经过点![]() 时,从
时,从![]() 的一侧
的一侧
进入另一侧),求函数![]() 的表达式.
的表达式.
湖北(文)
一、选择题(每小题5分)
4.函数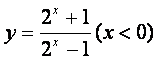 的反函数是( )
的反函数是( )
A.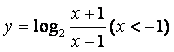 B.
B.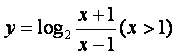
C.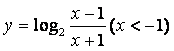 D.
D.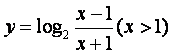
![]()
二、填空题(每小题5分)
13.已知函数![]() 的图象在点
的图象在点![]() 处的切线方程是
处的切线方程是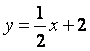 ,
,
则![]() ____.
____.
15.为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,
室内每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,
![]() 与
与![]() 的函数关系式为
的函数关系式为 (
(![]() 为常数),
为常数),
如图所示,根据图中提供的信息,回答下列问题: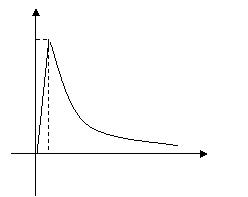
(I)从药物释放开始,每立方米空气中的含药量![]() (毫克)
(毫克)
与时间![]() (小时)之间的函数关系式为 .
(小时)之间的函数关系式为 .
(II)据测定,当空气中每立方米的含药量降低到![]() 毫克以下时,学生方可进教室,
毫克以下时,学生方可进教室,
那么从药物释放开始,至少需要经过 小时后,学生才能回到教室.
三、解答题
18.(本小题满分12分)
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量
可以增加,且每星期多卖出的商品件数与商品单价的降低值![]()
(单位:元,![]() )的平方成正比,已知商品单价降低2元时,
)的平方成正比,已知商品单价降低2元时,
一星期多卖出24件.
(I)将一个星期的商品销售利润表示成![]() 的函数;
的函数;
(II)如何定价才能使一个星期的商品销售利润最大?
19.(本小题满分12分)
设二次函数![]() ,方程
,方程![]() 的两根
的两根![]() 和
和![]() 满足
满足![]() .
.
(I)求实数![]() 的取值范围;
的取值范围;
(II)试比较![]() 与
与![]() 的大小.并说明理由.
的大小.并说明理由.
江苏
一、选择题(每小题5分)
8.设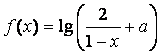 是奇函数,则使
是奇函数,则使![]() 的
的![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知二次函数![]() 的导数为
的导数为![]() ,
,![]() ,对于任意实数
,对于任意实数![]() ,
,
有![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题5分)
13.已知函数![]() 在区间
在区间![]() 上的最大值与最小值分别为
上的最大值与最小值分别为![]() ,
,![]() ,
,
则![]() _____.
_____.
16.某时钟的秒针端点![]() 到中心点
到中心点![]() 的距离为
的距离为![]() ,秒针均匀地绕点
,秒针均匀地绕点![]() 旋转,
旋转,
当时间![]() 时,点
时,点![]() 与钟面上标
与钟面上标![]() 的点
的点![]() 重合.将
重合.将![]() 两点间的距离
两点间的距离![]() 表
表
示成![]() 的函数,则
的函数,则![]() _____,其中
_____,其中![]() .
.
三、解答题
21.(本题满分16分)
已知![]() 是不全为零的实数,函数
是不全为零的实数,函数![]() ,
,![]() .
.
方程![]() 有实数根,且
有实数根,且![]() 的实数根都是
的实数根都是![]() 的根;反之,
的根;反之,
![]() 的实数根都是
的实数根都是![]() 的根.
的根.
(1)求![]() 的值;(3分)
的值;(3分)
(2)若![]() ,求
,求![]() 的取值范围;(6分)
的取值范围;(6分)
(3)若![]() ,
,![]() ,求
,求![]() 的取值范围.(7分)
的取值范围.(7分)
广东(文)
一、选择题(每小题5分)
3.若函数![]() ,则函数
,则函数![]() 在其定义域上是(
)
在其定义域上是(
)
A.单调递减的偶函数 B.单调递减的奇函数
C.单调递增的偶函数 D.单调递增的奇函数
5、客车从甲地以60km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,
然后以80km/h的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,
最后到达丙地所经过的路程s与时间t之间关系的图象中,正确的是( )
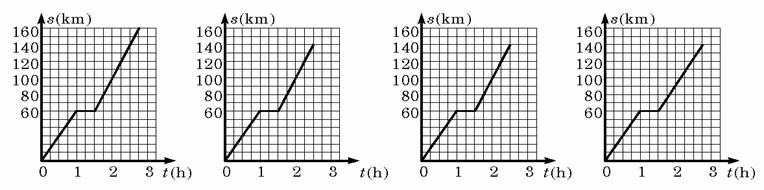
A. B. C. D.
二、填空题(每小题5分)
12.函数![]() 的单调递增区间是 .
的单调递增区间是 .
三、解答题
18.(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与
(吨)与
相应的生产能耗![]() (吨标准煤)的几组对照数据.
(吨标准煤)的几组对照数据.
|
|
|
|
|
|
|
|
|
|
|
|
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的
线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:![]() )
)
21.(本小题满分14分)
已知![]() 是实数,函数
是实数,函数![]() ,如果函数
,如果函数![]() 在区间
在区间![]() 上有零点,求
上有零点,求![]() 的取值范围.
的取值范围.
北京(文)
一、选择题(每小题5分)
2.函数![]() 的反函数的定义域为( )
的反函数的定义域为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.对于函数①![]() ,②
,②![]() ,③
,③![]() ,判断如下两个命题的真假:
,判断如下两个命题的真假:
命题甲:![]() 是偶函数;
是偶函数;
命题乙:![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
能使命题甲、乙均为真的所有函数的序号是( )
A.①② B.①③ C.② D.③
二、填空题(每小题5分)
14.已知函数![]() ,
,![]() 分别由下表给出
分别由下表给出
|
|
1 |
2 |
3 |
|
|
2 |
1 |
1 |
|
|
1 |
2 |
3 |
|
|
3 |
2 |
1 |
则![]() 的值为 ;当
的值为 ;当![]() 时,
时,![]() .
.
三、解答题
20.(本小题共14分)
已知函数![]() 与
与![]() 的图象相交于
的图象相交于![]() ,
,![]() ,
,![]() ,
,![]() 分别
分别
是![]() 的图象在
的图象在![]() 两点的切线,
两点的切线,![]() 分别是
分别是![]() ,
,![]() 与
与![]() 轴的交点.
轴的交点.
(I)求![]() 的取值范围;
的取值范围;
(II)设![]() 为点
为点![]() 的横坐标,当
的横坐标,当![]() 时,写出
时,写出![]() 以
以![]() 为自变量的函数式,
为自变量的函数式,
并求其定义域和值域;
(III)试比较![]() 与
与![]() 的大小,并说明理由(
的大小,并说明理由(![]() 是坐标原点).
是坐标原点).
上海(文)
一、填空题(每小题4分)
2.函数 的反函数
的反函数![]() .
.
8.某工程由![]() 四道工序组成,完成它们需用时间依次为
四道工序组成,完成它们需用时间依次为![]() 天.四道工
天.四道工
序的先后顺序及相互关系是:![]() 可以同时开工;
可以同时开工;![]() 完成后,
完成后,![]() 可以开工;
可以开工;![]()
完成后,![]() 可以开工.若该工程总时数为9天,则完成工序
可以开工.若该工程总时数为9天,则完成工序![]() 需要的天数
需要的天数![]() 最大是 .
最大是 .
三.解答题
19.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
已知函数 ,常数
,常数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)讨论函数![]() 的奇偶性,并说明理由.
的奇偶性,并说明理由.
山东(文)
一、选择题(每小题5分)
6.给出下列三个等式:![]() ,
, .
.
下列函数中不满足其中任何一个等式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.某班50名学生在一次百米测试中,成绩全部介
于13秒与19秒之间,将测试结果按如下方式分成六
组:每一组,成绩大于等于13秒且小于14秒;第二
组,成绩大于等于14秒且小于15秒;……第六组,
成绩大于等于18秒且小于等于19秒.右图是按上述
分组方法得到的频率分布直方图,设成绩小于17秒
的学生人数占全班人数的百分比为![]() ,成绩大于等于
,成绩大于等于
15秒且小于17秒的学生人数为![]() ,则从频率分布直方
,则从频率分布直方
图中可以分析出![]() 和
和![]() 分别为(
)
分别为(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.设函数![]() 与
与 的图象的交点为
的图象的交点为![]() ,
,
则![]() 所在的区间是(
)
所在的区间是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题4分)
13.设函数![]()
![]() ,则
,则![]() .
.
14.函数![]() 的图象恒过定点
的图象恒过定点![]() ,若点
,若点![]() 在直线
在直线![]() 上,
上,
则 的最小值为
.
的最小值为
.
三、解答题
19.(本小题满分12分)
本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用
不超过9万元,甲、乙电视台的广告收费标准分别为![]() 元/分钟和200元/分钟,规定
元/分钟和200元/分钟,规定
甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元
和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益
最大,最大收益是多少万元?
21.(本小题满分12分)
设函数![]() ,其中
,其中![]() .
.
证明:当![]() 时,函数
时,函数![]() 没有极值点;当
没有极值点;当![]() 时,函数
时,函数![]() 有且只有
有且只有
一个极值点,并求出极值.
江西(文)
一、选择题(每小题5分)
3.函数![]() 的定义域为( )
的定义域为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设![]() 在
在![]() 内单调递增,
内单调递增,![]() ,则
,则![]() 是
是![]() 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
二、填空题(每小题4分)
15.已知函数![]() 存在反函数
存在反函数![]() ,若函数
,若函数![]() 的图象经过点
的图象经过点![]() ,
,
则函数![]() 的图象必经过点 .
的图象必经过点 .
三、解答题
17.(本小题满分12分)
已知函数 满足
满足 .
.
(1)求常数![]() 的值;
的值;
(2)解不等式 .
.
陕西(文)
一、选择题(每小题5分)
2.函数![]() 的定义域为( )
的定义域为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设函数![]() 的反函数为
的反函数为![]() ,则函数
,则函数![]() 的图象是( )
的图象是( )

A. B. C. D.
12.某生物生长过程中,在三个连续时段内的增长量都相等,在各时段内平均增长
速度分别为![]() ,该生物在所讨论的整个时段内的平均增长速度为( )
,该生物在所讨论的整个时段内的平均增长速度为( )
A. B.
B. C.
C.![]() D.
D.
三、解答题
21.(本小题满分12分)
已知![]() 在区间
在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数,
上是减函数,
又 .
.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若在区间![]() 上恒有
上恒有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
安徽(文)
一、选择题(每小题5分)
4.下列函数中,反函数是其自身的函数为( )
A.![]() ,
,![]() B.
B.![]()
C.![]() D.
D.![]() ,
,![]()
7.图中的图象所表示的函数的解析式为( )
A.
![]()
![]()
1 2
第7题图

B.
![]()
C.
![]()
D.![]()
![]()
11.定义在![]() 上的函数
上的函数![]() 既是奇函数,又是周期函数,
既是奇函数,又是周期函数,![]() 是它的一个正周期.
是它的一个正周期.
若将方程![]() 在闭区间
在闭区间![]() 上的根的个数记为
上的根的个数记为![]() ,则
,则![]() 可能为( )
可能为( )
A.0 B.1 C.3 D.5
四川(文)
一、选择题(每小题5分)
(2)函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的图象大致是()

(11)某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资
不小于对项目乙投资的![]() 倍,且对每个项目的投资不能低于5万元,对项目甲每投
倍,且对每个项目的投资不能低于5万元,对项目甲每投
资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该
公司正确提财投资后,在两个项目上共可获得的最大利润为()
A.36万元 B.31.2万元 C.30.4万元 D.24万元
三、解答题
(20)(本小题满分12分)
设函数f(x)=ax3+bx+c(a≠0)为奇函数,其图象在点(1,f(1))处的切线
与直线x-6y-7=0垂直,导函数f'(x)的最小值为-12.
(Ⅰ)求a,b,c的值;
(Ⅱ)求函数f(x)的单调递增区间,并求函数f(x)在〔-1,3〕上的最大值和最小值.
海南宁夏(文)
二、填空题(每小题5分)
14.设函数![]() 为偶函数,则
为偶函数,则![]() .
.
三、解答题
19.(本小题满分12分)
设函数![]()
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)求![]() 在区间
在区间 的最大值和最小值.
的最大值和最小值.
全国卷Ⅰ(文)
一、选择题(每小题5分)
8、设![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值之差为
上的最大值与最小值之差为![]() ,则
,则![]() ( )
( )
A.![]() B.2 C.
B.2 C.![]() D.4
D.4
9、设![]() ,
,![]() 是定义在R上的函数,
是定义在R上的函数,![]() ,则“
,则“![]() ,
,![]() 均为偶函数”
均为偶函数”
是“![]() 为偶函数”的( )
为偶函数”的( )
A.充要条件 B.充分而不必要的条件
C.必要而不充分的条件 D.既不充分也不必要的条件
二、填空题(每小题5分)
(14)函数![]() 的图像与函数
的图像与函数![]() 的图像关于直线
的图像关于直线![]() 对称,
对称,
则![]() ____________.
____________.
三、解答题
(20)(本小题满分12分)
设函数![]() 在
在![]() 及
及![]() 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的![]() ,都有
,都有![]() 成立,求c的取值范围.
成立,求c的取值范围.
全国卷Ⅱ(文)
一、选择题(每小题5分)
9.把函数![]() 的图像按向量
的图像按向量![]() 平移,得到
平移,得到![]() 的图像,则
的图像,则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
三、解答题
22.(本小题满分12分)
已知函数
在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值,且
处取得极小值,且![]() .
.
(1)证明![]() ;
;
(2)若z=a+2b,求z的取值范围。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。