米高度成功的概率分别是
，
，福建（文）
三、解答题
18．（本小题满分12分）
甲、乙两名跳高运动员一次试跳米高度成功的概率分别是，，
且每次试跳成功与否相互之间没有影响，求：
（Ⅰ）甲试跳三次，第三次才成功的概率；
（Ⅱ）甲、乙两人在第一次试跳中至少有一人成功的概率；
（Ⅲ）甲、乙各试跳两次，甲比乙的成功次数恰好多一次的概率．
浙江（文）
一、选择题（每小题5分）
8．甲、乙两人进行乒乓球比赛，比赛规则为“3局2胜”，即以先赢2局者为胜，
根据经验，每局比赛中甲获胜的概率为
，则本次比赛甲获胜的概率是（
）
A．
B．
C．
D．
二、填空题（每小题4分）
13．某校有学生2000人，其中高三学生500人，为了解学生的身体素质情况，
彩用按年级分层抽样的方法，从该校学生中抽取一个200人的样本，
则样本中高三学生的人数为 ．
天津（文）
二、填空题（每小题4分）
（11）从一堆苹果中任取了20只，并得到它们的质量（单位：克）数据分布表如下：
|
分组 |
|
|
|
|
|
|
|
频数 |
1 |
2 |
3 |
10 |
|
1 |
则这堆苹果中，质量不小于120克的苹果数约占苹果总数的 ％．
三、解答题
（18）（本小题满分12分）
已知甲盒内有大小相同的3个红球和4个黑球，乙盒内有大小相同的5个红球和
4个黑球．现从甲、乙两个盒内各任取2个球．
（Ⅰ）求取出的4个球均为红球的概率；
（Ⅱ）求取出的4个球中恰有1个红球的概率；
辽宁（文）
一、选择题（每小题5分）
10．一个坛子里有编号为1，2，…，12的12个大小相同的球，其中1到6号球是红球，
其余的是黑球．若从中任取两个球，则取到的都是红球，且至少有1个球的号码是偶
数的概率为（ ）
A．
B．
C．
D．
三、解答题
17．（本小题满分12分）
某公司在过去几年内使用某种型号的灯管1000支，该公司对这些灯管的使用寿命
（单位：小时）进行了统计，统计结果如下表所示：
|
分组 |
[500，900) |
[900，1100) |
[1100，1300) |
[1300，1500) |
[1500，1700) |
[1700，1900) |
[1900， |
|
频数 |
48 |
121 |
208 |
223 |
193 |
165 |
42 |
|
频率 |
|
|
|
|
|
|
|
（I）将各组的频率填入表中；
（II）根据上述统计结果，计算灯管使用寿命不足1500小时的频率；
（III）该公司某办公室新安装了这种型号的灯管3支，若将上述频率作为概率，
试求至少有2支灯管的使用寿命不足1500小时的概率．
重庆（文）
一、选择题（每小题5分）
7．从5张100元，3张200元，2张300元的奥运预赛门票中任取3张，
则所取3张中至少有2张价格相同的概率为（ ）
A．
B．
C．
D．
三、解答题
17．（本小题满分13分．（Ⅰ）小问5分．（Ⅱ）小问8分．）
设甲、乙两人每次射击命中目标的概率分别为
和
，且各次射击相互独立．
（Ⅰ）若甲、乙各射击一次，求甲命中但乙未命中目标的概率；
（Ⅱ）若甲、乙各射击两次，求两人命中目标的次数相等的概率．
湖南（文）
三、解答题
17．（本小题满分12分）
某地区为下岗人员免费提供财会和计算机培训，以提高下岗人员的再就业能力，
每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训，已知参加
过财会培训的有60%，参加过计算机培训的有75%，假设每个人对培训项目的选
择是相互独立的，且各人的选择相互之间没有影响．
（I）任选1名下岗人员，求该人参加过培训的概率；
（II）任选3名下岗人员，求这3人中至少有2人参加过培养的概率．
湖北（文）
一、选择题（每小题5分）
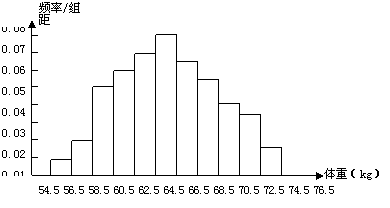
6．为了了解某学校学生的身体发育情况，抽查了该校100名高中男生的体重情况，
根据所得数据画出样本的频率分布直方图如右图所示．根据此图，估计该校2000名
高中男生中体重大于70.5公斤的人数为（ ）
A．300 B．360 C．420 D．450
7．将5本不同的书全发给4名同学，每名同学至少有一本书的概率是（ ）
A．
B．
C．
D．
二、填空题（每小题5分）
14．某篮球运动员在三分线投球的命中率是
，他投球10次，恰好投进3个球的概率为
．（用数值作答）
江苏
二、填空题（每小题5分）
12．某校开设
门课程供学生选修，其中
三门由于上课时间相同，至多选一门，
学校规定，每位同学选修
门，共有_____种不同的选修方案．（用数值作答）
三、解答题
17．（本题满分12分）
某气象站天气预报的准确率为
，计算（结果保留到小数点后第2位）：
（1）5次预报中恰有2次准确的概率；（4分）
（2）5次预报中至少有2次准确的概率；（4分）
（3）5次预报中恰有2次准确，且其中第3次预报准确的概率．（4分）
广东（文）
一、选择题（每小题5分）
8．在一个袋子中装有分别标注数字1，2，3，4，5的五个小球，这些小球除标注
的数字外完全相同．现从中随机取出2个小球，则取出的小球标注的数字之和
为3或6的概率是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
北京（文）
三、解答题
18．（本小题共12分）
某条公共汽车线路沿线共有11个车站（包括起点站和终点站），在起点站开出的一辆
公共汽车上有6位乘客，假设每位乘客在起点站之外的各个车站下车是等可能的．求：
（I）这6位乘客在其不相同的车站下车的概率；
（II）这6位乘客中恰有3人在终点站下车的概率；
上海（文）
一、填空题（每小题4分）
9．在五个数字
中，若随机取出三个数字，则剩下两个数字都是奇数的概率是
（结果用数值表示）．
三．解答题
18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．
近年来，太阳能技术运用的步伐日益加快．2002年全球太阳电池的年生产量达到
670兆瓦，年生产量的增长率为34%． 以后四年中，年生产量的增长率逐年递增2%
（如，2003年的年生产量的增长率为36%）．
（1）求2006年全球太阳电池的年生产量（结果精确到0.1兆瓦）；
（2）目前太阳电池产业存在的主要问题是市场安装量远小于生产量，2006年
的实际安装量为1420兆瓦．假设以后若干年内太阳电池的年生产量的增长率保持
在42%，到2010年，要使年安装量与年生产量基本持平（即年安装量不少于年生产
量的95%），这四年中太阳电池的年安装量的平均增长率至少应达到多少（结果精
确到0.1%）？
山东（文）
一、选择题（每小题5分）
12．设集合
，分别从集合
和
中随机取一个数
和
，确定平面
上的一个点
，记“点
落在直线
上”为事件
，
若事件
的概率最大，则
的所有可能值为（
）
A．3 B．4 C．2和5 D．3和4
江西（文）
一、选择题（每小题5分）
6．一袋中装有大小相同，编号分别为
的八个球，从中有放回地
每次取一个球，共取2次，则取得两个球的编号和不小于15的概率为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
三、解答题
19．（本小题满分12分）
栽培甲、乙两种果树，先要培育成苗，然后再进行移栽．已知甲、乙两种果树
成苗的概率分别为
，
，移栽后成活的概率分别为
，
．
（1）求甲、乙两种果树至少有一种果树成苗的概率；
（2）求恰好有一种果树能培育成苗且移栽成活的概率．
陕西（文）
一、选择题（每小题5分）
6．某商场有四类食品，其中粮食类、植物油类、动物性食品类及果蔬类分别
有40种、10种、30种、20种，现从中抽取一个容量为20的样本进行食品安全检测．
若采用分层抽样的方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是（ ）
Ａ．4 Ｂ．5 Ｃ．6 Ｄ．7
二、填空题(每小题4分)
15．安排3名支教教师去4所学校任教，每校至多2人，则不同的分配方案
共有 种．（用数字作答）
三、解答题
18．（本小题满分12分）
某项选拔共有四轮考核，每轮设有一个问题，能正确回答问题者进入下一轮考核，
否则即被淘汰．已知某选手能正确回答第一、二、三、四轮的问题的概率分别
为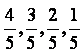
，且各轮问题能否正确回答互不影响．
（Ⅰ）求该选手进入第四轮才被淘汰的概率；
（Ⅱ）求该选手至多进入第三轮考核的概率．
（注：本小题结果可用分数表示）
安徽（文）
二、填空题（每小题4分）
14．在正方体上任意选择两条棱，则这两条棱相互平行的概率为 ．
三、解答题
19．（本小题满分13分）
在医学生物试验中，经常以果蝇作为试验对象．一个关有6只果蝇的笼子里，
不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把
笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔．
（I）求笼内恰好剩下1只果蝇的概率；
（II）求笼内至少剩下5只果蝇的概率．
四川（文）
一、选择题（每小题5分）
(3)某商场买来一车苹果，从中随机抽取了10个苹果，其重量（单位：克）
分别为：150，152，153，149，148，146，151，150，152，147，由此估计
这车苹果单个重量的期望值是（）
(A)150.2克 (B)149.8克 (C)149.4克 (D)147.8克
(9)用数字1，2，3，4，5可以组成没有重复数字，并且比20 000大的五位偶数共有（）
A.48个 B.36个 C.24个 D.18个
三、解答题
（17）（本小题满分12分）
厂家在产品出厂前，需对产品做检验，厂家对一般产品致冷商家的，商家符合
规定拾取一定数量的产品做检验，以决定是否验收这些产品.
（Ⅰ）若厂家库房中的每件产品合格的概率为0.3，从中任意取出4种进行检验，
求至少要1件是合格产品的概率.
(Ⅱ)若厂家发给商家20件产品，其中有3件不合格，按合同规定该商家从中任取2件，
来进行检验，只有2件产品合格时才接收这些产品，否则拒收，分别求出该商家计算
出不合格产品为1件和2件的概率，并求该商家拒收这些产品的概率。
海南宁夏（文）
三、解答题
20．（本小题满分12分）
设有关于
的一元二次方程
．
（Ⅰ）若
是从
四个数中任取的一个数，
是从
三个数中任取的一个数，
求上述方程有实根的概率．
（Ⅱ）若是从区间
任取的一个数，
是从区间
任取的一个数，
求上述方程有实根的概率．
全国卷Ⅰ（文）
一、选择题（每小题5分）
（5）甲、乙、丙
位同学选修课程，从门课程中，甲选修
门，乙、丙各选修
门，
则不同的选修方案共有（ ）
Ａ．
种 Ｂ．
种 Ｃ．
种
Ｄ．
种
二、填空题（每小题5分）
（13）从某自动包装机包装的食盐中，随机抽取
袋，测得各袋的质量分别为（单位：
）：
|
492 |
496 |
494 |
495 |
498 |
497 |
501 |
502 |
504 |
496 |
|
497 |
503 |
506 |
508 |
507 |
492 |
496 |
500 |
501 |
499 |
根据频率分布估计总体分布的原理，该自动包装机包装的袋装食盐质量
在497.5g～501.5g之间的概率约为_____．
三、解答题
（18）（本小题满分12分）
某商场经销某商品，顾客可采用一次性付款或分期付款购买．根据以往资料统计，
顾客采用一次性付款的概率是0.6，经销一件该商品，若顾客采用一次性付款，
商场获得利润200元；若顾客采用分期付款，商场获得利润250元．
（Ⅰ）求3位购买该商品的顾客中至少有1位采用一次性付款的概率；
（Ⅱ）求3位顾客每人购买1件该商品，商场获得利润不超过650元的概率．
全国卷Ⅱ（文）
二、填空题（每小题5分）
13．一个总体含有100个个体，以简单随机抽样方式从该总体中抽取一个容量
为5的样本，则指定的某个个体被抽到的概率为 ．
三、解答题
19．（本小题满分12分）
从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件
：
“取出的2件产品中至多有1件是二等品”的概率
．
（1）求从该批产品中任取1件是二等品的概率
；
（2）若该批产品共100件，从中任意抽取2件，求事件：“取出的2件产品中
至少有一件二等品”的概率
．
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。
)