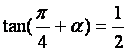 ,(1)求
,(1)求 的值。
的值。2004年
解答题
17. (本小题满分12分)
已知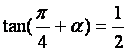 ,(1)求
,(1)求![]() 的值;(2)求
的值;(2)求 的值。
的值。
18. (本小题满分12分)
从4名男生和2名女生中任选3人参加演讲比赛,设随机变量![]() 表示
表示
所选3人中女生的人数。
(1)求![]() 的分布列;
的分布列;
(2)求![]() 的数学期望;
的数学期望;
(3)求“所选3人中女生人数![]() ”的概率。
”的概率。
19. (本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,
PD=DC,E是PC的中点,作EF⊥PB交PB于点F。
(1)证明PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C—PB—D的大小。
20. (本小题满分12分)
已知函数![]() 在
在![]() 处取得极值。
处取得极值。
(1)讨论![]() 和
和![]() 是函数
是函数![]() 的极大值还是极小值;
的极大值还是极小值;
(2)过点![]() 作曲线
作曲线![]() 的切线,求此切线方程。
的切线,求此切线方程。
21. (本小题满分12分)
已知定义在R上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:
![]() ,
,
![]() ,其中a为常数,k为非零常数。
,其中a为常数,k为非零常数。
(1)令![]()
![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(2)求数列![]() 的通项公式;
的通项公式;
(3)当![]() 时,求
时,求![]() 。
。
22. (本小题满分14分)
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(![]() )
)
的准线![]() 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点。
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点。
(1)求椭圆的方程及离心率;
(2)若![]() ,求直线PQ的方程;
,求直线PQ的方程;
(3)设![]() (
(![]() ),过点P且平行于准线
),过点P且平行于准线![]() 的直线与椭圆相交于
的直线与椭圆相交于
另一点M,证明![]() 。
。
2005年
解答题
(17)(本小题满分12分)
在![]() 中,
中,![]() 所对的边长分别为
所对的边长分别为![]() ,设
,设![]() 满足条件
满足条件
![]() 和
和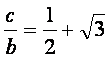 ,求
,求![]() 和
和![]() 的值
的值
(18)(本小题满分12分)
已知![]()
![]()
(Ⅰ)当![]() 时,求数列
时,求数列![]() 的前n项和
的前n项和![]()
(Ⅱ)求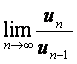
(19)(本小题满分12分)
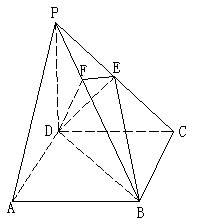
如图,在斜三棱柱![]() 中,
中,![]() ,
,
侧面![]() 与底面ABC所成的二面角为
与底面ABC所成的二面角为![]() ,E、F分别是棱
,E、F分别是棱![]() 的中点
的中点
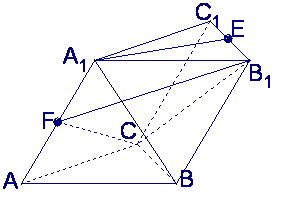 (Ⅰ)求
(Ⅰ)求![]() 与底面ABC所成的角
与底面ABC所成的角
(Ⅱ)证明![]() ∥平面
∥平面![]()
(Ⅲ)求经过![]() 四点的球的体积
四点的球的体积
(20)(本小题满分12)
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),
塔所在的山高OB=220(米),OA=200(米),
图中所示的山坡可视为直线![]() 且点P在直线
且点P在直线![]() 上,
上,
![]() 与水平地面的夹角为
与水平地面的夹角为![]() ,tan
,tan![]() =1/2试问此人
=1/2试问此人
距水平地面多高时,观看塔的视角∠BPC最大
(不计此人的身高)
(21)(本小题满分14分)
抛物线C的方程为![]() ,过抛物线C上一点P(x0,y0)(x0≠0)作斜率
,过抛物线C上一点P(x0,y0)(x0≠0)作斜率
为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互
不相同),且满足![]()
![]()
(Ⅰ)求抛物线C的焦点坐标和准线方程
(Ⅱ)设直线AB上一点M,满足![]() ,证明线段PM的中点在y轴上
,证明线段PM的中点在y轴上
(Ⅲ)当![]() =1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
![]() 的取值范围
的取值范围
(22)(本小题满分14分)
设函数![]() .
.
(Ⅰ)证明![]() ,其中为k为整数;
,其中为k为整数;
(Ⅱ)设![]() 为
为![]() 的一个极值点,证明
的一个极值点,证明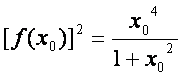 ;
;
(Ⅲ)设![]() 在(0,+∞)内的全部极值点按从小到大的顺序排列
在(0,+∞)内的全部极值点按从小到大的顺序排列![]() ,
,
证明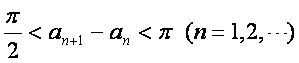
2006
解答题
(17)(本小题满分12分)
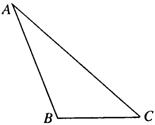
如图,在△ABC中,AC=2,BC=l,cosC=![]() .
.
(Ⅰ)求AB的值;
(Ⅱ)求sin(2A+C)的值.
(18)(本小题满分12分)
某射手进行射击训练,假设每次射击击中目标的概率为![]() ,
,
且各次射击的结果互不影响.
(Ⅰ)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);
(Ⅱ)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);
(Ⅲ)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.
(19)(本小题满分12分)
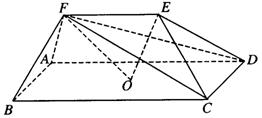
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,
面CDE是等边三角形,棱EF![]()
![]() BC.
BC.
(Ⅰ)证明FO∥平面CDE;
(Ⅱ)设BC=![]() CD,证明EO⊥平面CDF.
CD,证明EO⊥平面CDF.
(20)(本小题满分12分)
已知函数f(x)=4x3-3x2cosθ+![]() cosθ,其中x∈R,θ为参数,且0≤θ<2π.
cosθ,其中x∈R,θ为参数,且0≤θ<2π.
(Ⅰ)当cosθ=0时,判断函数f(x)是否有极值;
(Ⅱ)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数θ,函数f(x)在区间
(2a-1,a)内都是增函数,求实数α的取值范围.
(21)(本小题满分14分)
已知数列{xn}、{yn}满足x1=x2=1,y1=y2=2,并且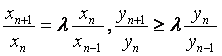
(![]() 为非零参数,n=2,3,4,…).
为非零参数,n=2,3,4,…).
(Ⅰ)若x1、x3、x5成等比数列,求参数![]() 的值;
的值;
(Ⅱ)当![]() >0时,证明
>0时,证明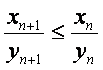 (n∈N*);
(n∈N*);
(Ⅲ)当![]() >1时,证明
>1时,证明 <
< (n∈N*).
(n∈N*).
(22)(本小题满分14分)
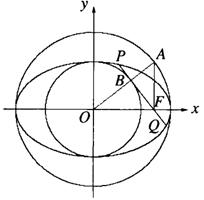
如图,以椭圆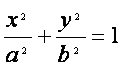 (a>b>0)的中心O为圆心,分别以a和b为
(a>b>0)的中心O为圆心,分别以a和b为
半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大
圆于第一象限内的点A.连结OA交小圆于点B.设直线BF是小圆的切线.
(Ⅰ)证明c2=ab,并求直线BF与y轴的交点M的坐标;
(Ⅱ)设直线BF交椭圆于P、Q两点,证明![]() ·
·![]() =
=![]() b2.
b2.
2007
解答题
17.(本小题满分12分)
已知函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ)求函数![]() 在区间
在区间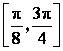 上的最小值和最大值.
上的最小值和最大值.
18.(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和
4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设![]() 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
19.(本小题满分12分)
如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,
![]() ,
,![]() 是
是![]() 的中点.
的中点.
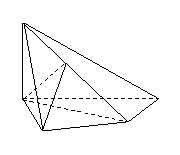 (Ⅰ)证明
(Ⅰ)证明![]() ;
;
(Ⅱ)证明![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
20.(本小题满分12分)
已知函数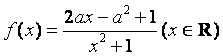 ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 的单调区间与极值.
的单调区间与极值.
21.(本小题满分14分)
在数列![]() 中,
中,![]() ,其中
,其中![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)证明存在![]() ,使得
,使得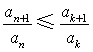 对任意
对任意![]() 均成立.
均成立.
22.(本小题满分14分)
设椭圆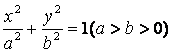 的左、右焦点分别为
的左、右焦点分别为![]() 是椭圆上的一点,
是椭圆上的一点,![]() ,
,
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)设![]() 为椭圆上的两个动点,
为椭圆上的两个动点,![]() ,过原点
,过原点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,
,
垂足为![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。