福建(理)
一、选择题(每小题5分)
2.数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() 等于(
)
等于(
)
A.1
B.![]() C.
C.![]() D.
D.![]()
9.把![]() 展开成关于
展开成关于![]() 的多项式,其各项系数和为
的多项式,其各项系数和为![]() ,
,
则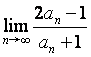 等于(
)
等于(
)
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
三、解答题
21.(本小题满分12分)
等差数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(Ⅰ)求数列![]() 的通项
的通项![]() 与前
与前![]() 项和
项和![]() ;
;
(Ⅱ)设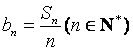 ,求证:数列
,求证:数列![]() 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
浙江(理)
三、解答题
(21)(本题15分)已知数列![]() 中的相邻两项
中的相邻两项![]() 是关于
是关于![]() 的方程
的方程
![]() 的两个根,且
的两个根,且![]() .
.
(I)求![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(II)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)记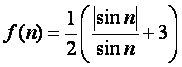 ,
,
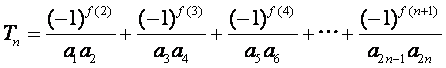 ,
,
求证:![]() .
.
天津(理)
一、选择题(每小题5分)
8.设等差数列![]() 的公差
的公差![]() 不为0,
不为0,![]() .若
.若![]() 是
是![]() 与
与![]() 的等比中项,则
的等比中项,则![]() ( )
( )
A.2 B.4 C.6 D.8
二、填空题(每小题4分)
11.若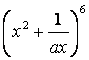 的二项展开式中
的二项展开式中![]() 的系数为
的系数为![]() ,则
,则![]() (用数字作答).
(用数字作答).
13.设等差数列![]() 的公差
的公差![]() 是2,前
是2,前![]() 项的和为
项的和为![]() ,则
,则 .
.
三、解答题
21.(本小题满分14分)
在数列![]() 中,
中,![]() ,其中
,其中![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)证明存在![]() ,使得
,使得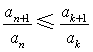 对任意
对任意![]() 均成立.
均成立.
辽宁(理)
一、选择题(每小题5分)
4.设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() (
)
(
)
A.63 B.45 C.36 D.27
三、解答题
21.(本小题满分12分)
已知数列![]() ,
,![]() 与函数
与函数![]() ,
,![]() ,
,![]() 满足条件:
满足条件:
![]() ,
,![]() .
.
(I)若![]() ,
,![]() ,
,![]() ,
,![]() 存在,求
存在,求![]() 的取值范围;
的取值范围;
(II)若函数![]() 为
为![]() 上的增函数,
上的增函数,![]() ,
,![]() ,
,![]() ,证明对任意
,证明对任意![]() ,
,
![]() (用
(用![]() 表示).
表示).
重庆(理)
一、选择题(每小题5分)
1.若等比数列![]() 的前
的前![]() 项和
项和![]() 且
且![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.若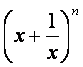 展开式的二项式系数之和为
展开式的二项式系数之和为![]() ,则展开式的常数项为( )
,则展开式的常数项为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若![]() 是
是![]() 与
与![]() 的等比中项,则
的等比中项,则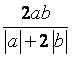 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题4分)
14.设![]() 为公比
为公比![]() 的等比数列,若
的等比数列,若![]() 和
和![]() 是方程
是方程![]() 的两根,
的两根,
则![]() ______.
______.
三、解答题
21.(本小题满分12分,其中(Ⅰ)小问5分,(Ⅱ)小问7分.)
已知各项均为正数的数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 满足
满足![]() ,并记
,并记![]() 为
为![]() 的前
的前![]() 项和,求证:
项和,求证:
![]() .
.
湖南(理)
三、解答题
21.(本小题满分13分)
已知![]() (
(![]() )是曲线
)是曲线![]() 上的点,
上的点,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,
且满足![]() ,
,![]() ,
,![]() ….
….
(I)证明:数列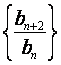 (
(![]() )是常数数列;
)是常数数列;
(II)确定![]() 的取值集合
的取值集合![]() ,使
,使![]() 时,数列
时,数列![]() 是单调递增数列;
是单调递增数列;
(III)证明:当![]() 时,弦
时,弦![]() (
(![]() )的斜率随
)的斜率随![]() 单调递增.
单调递增.
湖北(理)
一、选择题(每小题5分)
1.如果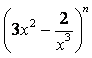 的展开式中含有非零常数项,则正整数
的展开式中含有非零常数项,则正整数![]() 的最小值为( )
的最小值为( )
A.3 B.5 C.6 D.10
6.若数列![]() 满足
满足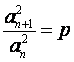 (
(![]() 为正常数,
为正常数,![]() ),则称
),则称![]() 为“等方比数列”.
为“等方比数列”.
甲:数列![]() 是等方比数列;
乙:数列
是等方比数列;
乙:数列![]() 是等比数列,则(
)
是等比数列,则(
)
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
8.已知两个等差数列![]() 和
和![]() 的前
的前![]() 项和分别为A
项和分别为A![]() 和
和![]() ,且
,且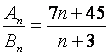 ,
,
则使得![]() 为整数的正整数
为整数的正整数![]() 的个数是(
)
的个数是(
)
A.2 B.3 C.4 D.5
三、解答题
21.(本小题满分14分)
已知![]() 为正整数,
为正整数,
(I)用数学归纳法证明:当![]() 时,
时,![]() ;
;
(II)对于![]() ,已知
,已知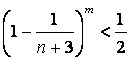 ,求证
,求证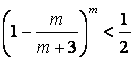 ,
,
求证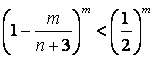 ,
,![]() ;
;
(III)求出满足等式![]() 的所有正整数
的所有正整数![]() .
.
江苏
一、选择题(每小题5分)
7.若对于任意的实数![]() ,有
,有![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
三、解答题
20.(本题满分16分)
已知![]() 是等差数列,
是等差数列,![]() 是公比为
是公比为![]() 的等比数列,
的等比数列,![]() ,
,![]() ,
,
记![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)若![]() (
(![]() 是大于
是大于![]() 的正整数),求证:
的正整数),求证:![]() ;(4分)
;(4分)
(2)若![]() (
(![]() 是某个正整数),求证:
是某个正整数),求证:![]() 是整数,且数列
是整数,且数列![]() 中的每一项
中的每一项
都是数列![]() 中的项;(8分)
中的项;(8分)
(3)是否存在这样的正数![]() ,使等比数列
,使等比数列![]() 中有三项成等差数列?
中有三项成等差数列?
若存在,写出一个![]() 的值,并加以说明;若不存在,请说明理由.(4分)
的值,并加以说明;若不存在,请说明理由.(4分)
广东(理)
一、选择题(每小题5分)
5.已知数列![]() 的前
的前![]() 项和
项和![]() ,第
,第![]() 项满足
项满足![]() ,则
,则![]() (
)
(
)
A.9 B.8 C.7 D.6
三、解答题
21.(本小题满分14分)
已知函数![]() ,
,![]() 是方程
是方程![]() 的两个根(
的两个根(![]() ),
),![]() 是
是![]() 的导数,
的导数,
设![]() ,
,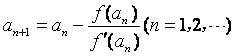 .
.
(1)求![]() 的值;
的值;
(2)证明:对任意的正整数![]() ,都有
,都有![]() ;
;
(3)记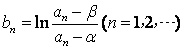 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
北京(理)
二、填空题(每小题5分)
10.若数列![]() 的前
的前![]() 项和
项和![]() ,则此数列的通项公式为
;
,则此数列的通项公式为
;
数列![]() 中数值最小的项是第
项.
中数值最小的项是第
项.
三、解答题
15.(本小题共13分)
数列![]() 中,
中,![]() ,
,![]() (
(![]() 是常数,
是常数,![]() ),
),
且![]() 成公比不为
成公比不为![]() 的等比数列.
的等比数列.
(I)求![]() 的值;
的值;
(II)求![]() 的通项公式.
的通项公式.
上海(理)
三、解答题
20.(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分6分,
第3小题满分9分.
如果有穷数列![]() (
(![]() 为正整数)满足条件
为正整数)满足条件![]() ,
,![]() ,
,
…,![]() ,即
,即![]() (
(![]() ),我们称其为“对称数列”.例如,
),我们称其为“对称数列”.例如,
由组合数组成的数列![]() 就是“对称数列”.
就是“对称数列”.
(1)设![]() 是项数为7的“对称数列”,其中
是项数为7的“对称数列”,其中![]() 是等差数列,且
是等差数列,且![]() ,
,
![]() .依次写出
.依次写出![]() 的每一项;
的每一项;
(2)设![]() 是项数为
是项数为![]() (正整数
(正整数![]() )的“对称数列”,其中
)的“对称数列”,其中![]() 是
是
首项为![]() ,公差为
,公差为![]() 的等差数列.记
的等差数列.记![]() 各项的和为
各项的和为![]() .当
.当![]() 为何值时,
为何值时,
![]() 取得最大值?并求出
取得最大值?并求出![]() 的最大值;
的最大值;
(3)对于确定的正整数![]() ,写出所有项数不超过
,写出所有项数不超过![]() 的“对称数列”,
的“对称数列”,
使得![]() 依次是该数列中连续的项;当
依次是该数列中连续的项;当![]()
![]() 时,求其中一个
时,求其中一个
“对称数列”前![]() 项的和
项的和![]() .
.
山东(理)
三、解答题
(17)(本小题满分12分)
设数列![]() 满足
满足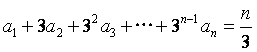 ,
,![]() .
.
(Ⅰ)求数列![]() 的通项;
的通项;
(Ⅱ)设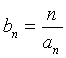 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
江西(理)
一、选择题(每小题5分)
4.已知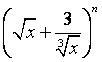 展开式中,各项系数的和与其各项二项式系数的和之比为
展开式中,各项系数的和与其各项二项式系数的和之比为![]() ,
,
则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题4分)
14.已知数列![]() 对于任意
对于任意![]() ,有
,有![]() ,若
,若![]() ,则
,则 ![]() .
.
三、解答题
22.(本小题满分14分)
设正整数数列![]() 满足:
满足:![]() ,且对于任何
,且对于任何![]() ,有
,有 .
.
(1)求![]() ,
,![]() ;
;
(3)求数列![]() 的通项
的通项![]() .
.
陕西(理)
一、选择题(每小题5分)
5.各项均为正数的等比数列![]() 的前
的前![]() 项和为
项和为![]() 为,若
为,若![]() ,
,![]() ,
,
则![]() 等于(
)
等于(
)
A.80 B.30 C.26 D.16
三、解答题
22.(本小题满分12分)
已知各项全不为零的数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且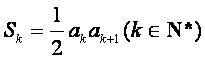 ,其中
,其中![]() .
.
(I)求数列![]() 的通项公式;
的通项公式;
(II)对任意给定的正整数![]() ,数列
,数列![]() 满足
满足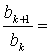
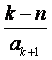 (
(![]() ),
),
![]() ,求
,求![]() .
.
安徽(理)
三、解答题
21.(本小题满分14分)
某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为![]() ,
,
以后每年交纳的数目均比上一年增加![]() ,因此,历年所交纳的储备金数目
,因此,历年所交纳的储备金数目
![]() 是一个公差为
是一个公差为![]() 的等差数列.与此同时,国家给予优惠的计息政策,
的等差数列.与此同时,国家给予优惠的计息政策,
不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为![]() ,那么,
,那么,
在第![]() 年末,第一年所交纳的储备金就变为
年末,第一年所交纳的储备金就变为![]() ,第二年所交纳的储备金就
,第二年所交纳的储备金就
变为![]() ,
,![]() .以
.以![]() 表示到第
表示到第![]() 年末所累计的储备金总额.
年末所累计的储备金总额.
(Ⅰ)写出![]() 与
与![]() 的递推关系式;
的递推关系式;
(Ⅱ)求证:![]() ,其中
,其中![]() 是一个等比数列,
是一个等比数列,![]() 是一个等差数列.
是一个等差数列.
四川(理)
三、解答题
(21)(本小题满分12分)
已知函数![]() ,设曲线
,设曲线![]() 在点
在点![]() 处的切线与X轴的交点
处的切线与X轴的交点![]() ,
,
其中x1为正实数。
(Ⅰ)用xn表示xn+1;
(Ⅱ)求证:对一切正整数n,![]() 的充要条件是
的充要条件是![]() ;
;
(Ⅲ)若x1=4,记 ,证明数列{an}成等比数列,并求数列{an}的通项公式。
,证明数列{an}成等比数列,并求数列{an}的通项公式。
海南宁夏(理)
一、选择题(每小题5分)
4.已知![]() 是等差数列,
是等差数列,![]() ,其前10项和
,其前10项和![]() ,
,
则其公差![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() 成等比数列,
成等比数列,
则 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
全国卷(Ⅰ)理
一、选择题(每小题5分)
(10) 的展开式中,常数项为
的展开式中,常数项为![]() ,则
,则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题5分)
(15)等比数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() 的公比为 .
的公比为 .
三、解答题
(22)(本小题满分12分)
已知数列![]() 中
中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 中
中![]() ,
, ,
,![]() ,
,
证明:![]() ,
,![]() .
.
全国卷(Ⅱ)理
二、填空题(每小题5分)
13. 的展开式中常数项为
.(用数字作答)
的展开式中常数项为
.(用数字作答)
16.已知数列的通项![]() ,其前
,其前![]() 项和为
项和为![]() ,则
,则 .
.
三、解答题
21.(本小题满分12分)
设数列![]() 的首项
的首项![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,证明
,证明![]() ,其中
,其中![]() 为正整数.
为正整数.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。