 .
.三、解答题
22.(本小题满分14分)
设正整数数列![]() 满足:
满足:![]() ,且对于任何
,且对于任何![]() ,有
,有 .
.
(1)求![]() ,
,![]() ;
;
(3)求数列![]() 的通项
的通项![]() .
.
解:(1)据条件得 ①
①
当![]() 时,由
时,由 ,即有
,即有 ,
,
解得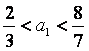 .因为
.因为![]() 为正整数,故
为正整数,故![]() .
.
当![]() 时,由
时,由 ,
,
解得![]() ,所以
,所以![]() .
.
(2)方法一:由![]() ,
,![]() ,
,![]() ,猜想:
,猜想:![]() .
.
下面用数学归纳法证明.
1![]() 当
当![]() ,
,![]() 时,由(1)知
时,由(1)知![]() 均成立;
均成立;
2![]() 假设
假设![]() 成立,则
成立,则![]() ,则
,则![]() 时
时
由①得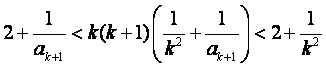
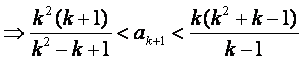

因为![]() 时,
时,![]() ,所以
,所以 .
.
![]() ,所以
,所以 .
.
又![]() ,所以
,所以![]() .
.
故![]() ,即
,即![]() 时,
时,![]() 成立.
成立.
由1![]() ,2
,2![]() 知,对任意
知,对任意![]() ,
,![]() .
.
(2)方法二:
由![]() ,
,![]() ,
,![]() ,猜想:
,猜想:![]() .
.
下面用数学归纳法证明.
1![]() 当
当![]() ,
,![]() 时,由(1)知
时,由(1)知![]() 均成立;
均成立;
2![]() 假设
假设![]() 成立,则
成立,则![]() ,则
,则![]() 时
时
由①得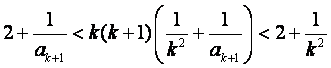
即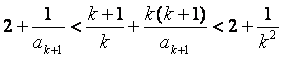 ②
②
由②左式,得 ,即
,即![]() ,因为两端为整数,
,因为两端为整数,
则![]() .于是
.于是![]() ③
③
又由②右式, .
.
则![]() .
.
因为两端为正整数,则![]() ,
,
所以 .
.
又因![]() 时,
时,![]() 为正整数,则
为正整数,则![]() ④
④
据③④![]() ,即
,即![]() 时,
时,![]() 成立.
成立.
由1![]() ,2
,2![]() 知,对任意
知,对任意![]() ,
,![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。