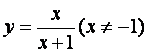 的反函数是(
)
的反函数是(
)福建(文)
一、选择题(每题5分)
(6)函数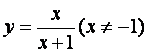 的反函数是(
)
的反函数是(
)
(A)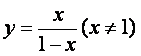 (B)
(B)
(C)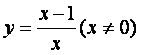 (D)
(D)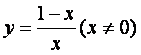
(12)已知![]() 是周期为2的奇函数,当
是周期为2的奇函数,当![]() 时,
时,![]()
设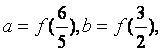
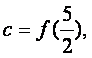 则(
)
则(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题(每题4分)
(16)已知函数![]() 在区间
在区间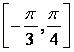 上的最小值是
上的最小值是![]() ,
,
则![]() 的最小值是
。
的最小值是
。
(21)(本小题满分12分)
已知![]() 是二次函数,不等式
是二次函数,不等式![]() 的解集是
的解集是![]() 且
且![]() 在
在
区间![]() 上的最大值是12。
上的最大值是12。
(I)求![]() 的解析式;
的解析式;
(II)是否存在实数![]() 使得方程
使得方程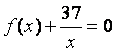 在区间
在区间![]() 内
内
有且只有两个不等的实数根?若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
浙江(文)
一、选择题(每小题5分)
(6)函数f(x)=x3-3x2+2在区间[-1,1]上的最大值是()
(A)-2 (B)0 (C)2 (D)4
(10)对a,b∈R,记max{a,b}=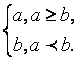 函数f(x)=max{|x+1|,|x-2|}
函数f(x)=max{|x+1|,|x-2|}
(x∈R)的最小值是()
(A)0 (B)![]() (C)
(C)![]() (D)3
(D)3
三、解答题
(20)设f(x)=3ax2+2bx+c,若a+b+c=0,f(0)f(1)>0,求证:
(Ⅰ)方程f(x)=0有实根;
(Ⅱ)-2<![]() <-1;
<-1;
(Ⅲ)设x1,x2是方程f(x)=0的两个实根,则![]() ≤|x1-x2|<
≤|x1-x2|<![]() .
.
天津(文)
一、选择题(每小题5分)
(6)函数y=![]() (x<0)的反函数是()
(x<0)的反函数是()
(A)y=![]() (x<0)
(B)y=-
(x<0)
(B)y=-![]() (x<0)
(x<0)
(C)y=![]() (x>2)
(D)y=-
(x>2)
(D)y=-![]() (x>2)
(x>2)
(10)如果函数f(x)=ax(ax-3a2-1)(a>0且a≠1)在区间[0,+∞)
上是增函数,那么实数a的取值范围是()
(A)(0,![]() ] (B)[
] (B)[![]() ,1) (C)(1,
,1) (C)(1,![]() ] (D)[
] (D)[![]() ,+∞)
,+∞)
二、填空题(每小题4分)
(15)某公司一年购买某种货物400吨,每次都购买x吨,运费为4万元/次,
—年的总存储费用为4x万元,要使—年的总运费与总存储费用之和最小,
则x=___________吨.解答
三、解答题
(20)(本小题满分12分)
已知函数f(x)=4x3-3x2cosθ+![]() ,其中x∈R,θ为参数,且0≤θ≤
,其中x∈R,θ为参数,且0≤θ≤![]() .
.
(Ⅰ)当cosθ=0时,判断函数f(x)是否有极值;
(Ⅱ)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数θ,函数f(x)在区间(2a-1,a)
内都是增函数,求实数a的取值范围.
江苏
三、解答题
(20)(本小题满分16分,第一小问4分,第二小问满分6分,第三小问满分6分)
设a为实数,设函数![]() 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=![]() ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足![]() 的所有实数a
的所有实数a
辽宁(文)
一、选择题(每题5分)
3.设![]() 是
是![]() 上的任意函数,下列叙述正确的是( )
上的任意函数,下列叙述正确的是( )
A.![]() 是奇函数
B.
是奇函数
B.![]() 是奇函数
是奇函数
C.![]() 是偶函数
D.
是偶函数
D.![]() 是偶函数
是偶函数
二、填空题(每题4分)
14.设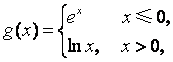 则
则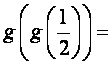 .
.
三、解答题
21.(本小题满分12分)
已知函数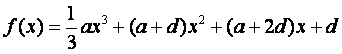 ,
,![]() ,
,
其中![]() ,设
,设![]() 为
为![]() 的极小值点,
的极小值点,![]() 为
为![]() 的极值点,
的极值点,![]() ,
,
并且![]() ,将点
,将点![]() 依次记为
依次记为![]() .
.
(1)求![]() 的值;
的值;
(2)若四边形![]() 为梯形且面积为1,求
为梯形且面积为1,求![]() 的值.
的值.
重庆(文)
一、选择题(每小题5分)
(6)设函数y=f(x)的反函数为x=f-1(x),且y=f(2x-1)的图象过
点(![]() ,1),则y=f--1(x)的图象必过点()
,1),则y=f--1(x)的图象必过点()
(A)(![]() ,1) (B)(1,
,1) (B)(1,![]() )
)
(C)(1,0) (D)(0,1)
解答
三、解答题
(19)(本小题满分12分)
设函数f(x)=x3-3ax2+3bx的图象与直线12x+y-1=0相切于点(1,-11).
(Ⅰ)求a,b的值;
(Ⅱ)讨论函数f(x)的单调性.
(21)(本小题满分12分)
已知定义域为R的函数f(x)=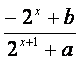 是奇函数.
是奇函数.
(Ⅰ)求a,b的值;
(Ⅱ)若对任意t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,
求k的取值范围.
湖南(文)
一、选择题(每题5分)
1.函数y=![]() 的定义域是(
)
的定义域是(
)
A.![]() B.(0,+∞)
C.(1,+∞)
D.
B.(0,+∞)
C.(1,+∞)
D.![]()
5.“a=1”是“函数f(x)=|x-a|在区间![]() 上为增函数”的(
)
上为增函数”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
二、填空题(每题4分)
15.若f(x)=asin(x+![]() )+3sin(x-
)+3sin(x-![]() )是偶函数,则a=
.
)是偶函数,则a=
.
三、解答题
19.(本小题满分14分)
已知函数f(x)=ax3-3x2+1-![]() .
.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若曲线y=f(x)上两点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,
求实数a的取值范围.
湖北(文)
一、选择题(每题5分)
7.设f(x)=lg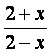 ,则f(
,则f(![]() )+f(
)+f(![]() )的定义域为(
)
)的定义域为(
)
A.(-4,0)∪(0,4) B.(-4,-1)∪(1,4)
C.(-2,-1)∪(1,2) D.(-4,-2)∪(2,4)
三、解答题
19.(本小题满分12分)
设函数f(x)=x3-ax2+bx+c在x=1处取得极值-2,试用c表示a和b,并求f(x)
的单调区间。
广东
一、选择题(每题5分)
1.函数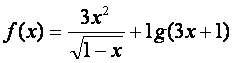 的定义域是()
的定义域是()
A.(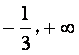 ) B.(
) B.(![]() ) C.(
) C.(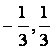 ) D.(
) D.(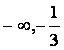 )
)
3.下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.函数![]() 的反函数y=f-1(x)的图像与y轴交于点P(0,2)(如图),
的反函数y=f-1(x)的图像与y轴交于点P(0,2)(如图),
则方程f(x)=0在![]() 上的根是x=()
上的根是x=()
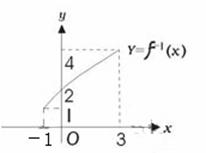
A.4 B.3 C.2 D.1
三、解答题
18.(本小题满分14分)
设函数f(x)=-x3+3x+2分别在x1、x2处取得极小值、极大值。xoy平面
上点A、B的坐标分别为(x1,f(x1))、(x2,f(x2))。该平面上动点P满
足![]() ,点Q是点P关于直线y=2(x-4)的对称点,求:
,点Q是点P关于直线y=2(x-4)的对称点,求:
(Ⅰ)点A、B的坐标:
(Ⅱ)动点Q的轨迹方程。
20.(本小题满分12分)
A是由定义在[2,4]上且满足如下条件的函数![]() (x)组成的集合:
(x)组成的集合:
①对任意的![]() 都有
都有![]() (2x)
(2x)![]() ;②存在常数L(0<L<1),
;②存在常数L(0<L<1),
使得对任意的x1,x2![]() [1,2],都有|
[1,2],都有|![]() (2x1)-
(2x1)-![]() (2x2)|
(2x2)|![]() .
.
(Ⅰ)设![]() (x)=
(x)=![]() 证明:
证明:![]() (x)
(x)![]() A:
A:
(Ⅱ)设![]() (x)
(x)![]() ,如果存在x0
,如果存在x0![]() (1,2),使得x0=
(1,2),使得x0=![]() (2x0),
(2x0),
那么这样的x0是唯一的:
(Ⅲ)设![]()
![]() 任取x1
任取x1![]() (1,2),令xn+1=
(1,2),令xn+1=![]() (2xn),n=1,2……证明:给定
(2xn),n=1,2……证明:给定
正整数k,对任意的正整数p,成立不等式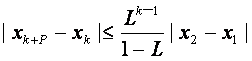 。
。
北京(文)
一、选择题(每题5分)
(2)函数y=1+cosx的图象( )
(A)关于x轴对称 (B)关于y轴对称
(C)关于原点对称
(D)关于直线x=![]() 对称
对称
(5)已知f(x)=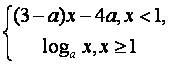 是(-∞,+∞)上的增函数,那么a的取值
是(-∞,+∞)上的增函数,那么a的取值
范围是( )
(A)(1,+∞) (B)(-∞,3)
(C)[![]() ,3)
(D)(1,3)
,3)
(D)(1,3)
二、填空题(每题4分)
(11)已知函数f(x)=ax-4a+3反函数的图象经过点(-1,2),那么a的值等于_____.
三、解答题
(16)(本小题共13分)
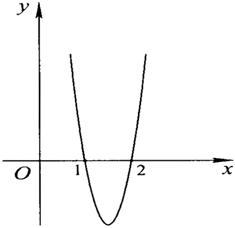
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经
过点(1,0),(2,0),如图所示.求:
(Ⅰ)x0的值;
(Ⅱ)a,b,c的值.
上海(文)
一、填空题(每小题4分)
3.若函数![]() =
=![]() (
(![]() >0,且
>0,且![]() ≠1)的反函数的图像过点(2,-1),
≠1)的反函数的图像过点(2,-1),
则![]() =
.解答
=
.解答
8.方程log3(x2-10)=1+log3x的解是_____________. 解答
三、解答题
22.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,
第3小题满分8分.
已知函数y=x+![]() 有如下性质,如果常数a>0,那么该函数在
有如下性质,如果常数a>0,那么该函数在![]() ]上是
]上是
减函数,在[![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)如果函数y=x+![]() 在(0,4]上是减函数,在[4,+∞)上是增函数,
在(0,4]上是减函数,在[4,+∞)上是增函数,
求实常数b的值;
(2)设常数c∈[1,4],求函数f(x)=x+![]() (1≤x≤2)的最大值和最小值;
(1≤x≤2)的最大值和最小值;
(3)当n是正整数时,研究函数g(x)=xn-![]() (c>0)的单调性,并说明理由.
(c>0)的单调性,并说明理由.
山东(文)
一、选择题(每小题5分)
(2)设
(A)0 (B)1 (C)2 (D)3
(3)函数y=1+ax(0<a<1)的反函数的图象大致是( )

(5)已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),则f(6)的值为()
(A)-1 (B)0 (C)1 (D)2
三、解答题
(17)(本小题满分12分)
设函数f(x)=![]()
(Ⅰ)求f(x)的单调区间;
(Ⅱ) 讨论f(x)的极值.
江西(文)
一、选择题(每题5分)
5.对于R上可导的任意函数f(x),若满足(x-1)f′(x)≥0,则必有( )
A.f(0)+f(2)<2f(1) B.f(0)+f(2)≤2f(1)
C.f(0)+f(2)≥2f(1) D.f(0)+f(2)>2f(1)
二、填空题(每题4分)
14.设f(x)=log3(x+6)的反函数为f-1(x),若[f-1(m)+6]·[f-1(n)+6]=27,
则f(m+n)=______.
三、解答题
17.(本小题满分12分)
已知函数f(x)=x3+ax2+bx+c在x=-![]() 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
陕西(文)
一、选择题(每小题5分)
2.函数f(x)= (x∈R)的值域是()
(x∈R)的值域是()
A.[0,1] B.[0,1) C.(0,1] D.(0,1)
4.设函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(0,0),
其反函数过点(1,2),则a+b等于()
A.3 B.4 C.5 D.6
7.设x、y为正数,则有 的最小值为()
的最小值为()
A.15 B.12 C.9 D.6
9.已知函数f(x)=ax2+2ax+4(a>0)。若x1<x2,x1+x2=0,则()
A.f(x1)>f(x2) B.f(x1)=f(x2)
C.f(x1)<f(x2) D.f(x1)与f(x2)的大小不能确定
12.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),
接收方由密文→明文(解密)。已知加密规则为:明文a,b,c,d对应密文a+2b,
2b+c,2c+3d,4d。例如,明文1,2,3,4对应密文5,7,18,16。当接收方
收到密文14,9,23,28时,则解密得到的明文为()
A.1,6,4,7 B.4,6,1,7
C.7,6,1,4 D.6,4,1,7
三、解答题
22.(本小题满分12分)
设![]() (k≥0)
(k≥0)
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)若函数![]() 的极小值大于0,求k的取值范围.
的极小值大于0,求k的取值范围.
安徽(文)
一、选择题(每题5分)
(3)函数![]() 的反函数是( )
的反函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(8)对于函数 ,下列结论正确的是(
)
,下列结论正确的是(
)
A.有最大值而无最小值 B.有最小值而无最大值
C.有最大值且有最小值 D.既无最大值又无最小值
(9)将函数![]() 的图象按向量
的图象按向量 平移,平移后的图象如图所示,
平移,平移后的图象如图所示,
则平移后的图象所对应函数的解析式是( )

A. B.
B.
C.![]() D.
D.![]()
二、填空题(每题4分)
(15)函数![]() 对于任意实数
对于任意实数![]() 满足条件
满足条件 ,若
,若![]()
则![]() __________。
__________。
三、解答题
(20)(本大题满分12分)设函数![]() ,已知
,已知
![]() 是奇函数。
是奇函数。
(Ⅰ)求![]() 、
、![]() 的值。
的值。
(Ⅱ)求![]() 的单调区间与极值。
的单调区间与极值。
四川(文)
一、选择题(每小题5分)
(2)函数![]() 的反函数是()
的反函数是()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
三、解答题
(21)(本大题满分12分)
已知函数![]() ,其中
,其中![]() 是
是![]() 的导函数
的导函数
(Ⅰ)对满足![]() 的一切
的一切![]() 的值,都有
的值,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() ,当实数
,当实数![]() 在什么范围内变化时,函数
在什么范围内变化时,函数![]() 的图象与
的图象与
直线![]() 只有一个公共点
只有一个公共点
全国卷(Ⅰ)文
一、选择题(每题5分)
(3)已知函数y=ex的图像与函数y=f(x)的图像关于直线y=x对称,则( )
(A)f(2x)=e![]()
![]() (x
(x![]() R)
(B)f(2x)=ln2·lnx(x>0)
R)
(B)f(2x)=ln2·lnx(x>0)
(C)f(2x)=2e![]() (x
(x![]() R)
(D)f(2x)=lnx+ln2(x>0)
R)
(D)f(2x)=lnx+ln2(x>0)
(6)函数f(x)=tan(x+![]() )的单调增区间为( )
)的单调增区间为( )
(A)(kπ-![]() ,kπ+
,kπ+![]() ),k
),k![]() (B)(kπ,(k+1)π),
k
(B)(kπ,(k+1)π),
k![]()
(C)(kπ-![]() ,kπ+
,kπ+![]() ),
k
),
k![]() (D)(kπ-
(D)(kπ-![]() ,kπ+
,kπ+![]() ),k
),k![]()
(13)已知函数f(x)=a- .若f(x)为奇函数,则a=
.若f(x)为奇函数,则a=
(22)(本小题满分14分)
设a为实数,函数f(x)=x![]() -ax
-ax![]() +(a
+(a![]() -1)x在(-
-1)x在(-![]() ,0)和(1,+
,0)和(1,+![]() )都是增函数,
)都是增函数,
求a的取值范围.
全国卷(Ⅱ)文
一、选择题(每小题5分)
(4)如果函数![]() 的图像与函数
的图像与函数![]() 的图像关于坐标原点对称,
的图像关于坐标原点对称,
则![]() 的表达式为(
)
的表达式为(
)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(8)已知函数![]() ,则
,则![]() 的反函数为()
的反函数为()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
三、解答题
(21)(本小题满分为14分)
设![]() ,函数
,函数![]() 若
若![]() 的解集为A,
的解集为A,
![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。