福建(理)
一、 选择题(每题5分)
(8)函数![]() 的反函数是(
)
的反函数是(
)
(A)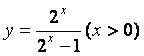 (B)
(B)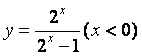
(C) (D)
(D)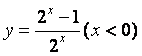
(9)已知函数![]() 在区间
在区间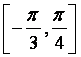 上的最小值是
上的最小值是![]() ,
,
则![]() 的最小值等于(
)
的最小值等于(
)
(A)![]() (B)
(B)![]() (C)2 (D)3
(C)2 (D)3
三、解答题
(21)(本小题满分12分)
已知函数![]()
(I)求![]() 在区间
在区间![]() 上的最大值
上的最大值![]()
(II)是否存在实数![]() 使得
使得![]() 的图象与
的图象与![]() 的图象有且只有三
的图象有且只有三
个不同的交点?若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
浙江(理)
一、选择题(每小题5分)
(10)函数![]() 则这样的函数个数共有()
则这样的函数个数共有()
(A)1个 (B)4个 (C)8个 (D)10个
二、填空题(每小题4分)
(12)对 函数
函数![]()
的是小值是______。
三、解答题
(16)设![]() :
:
(Ⅰ) ;
;
(Ⅱ)方程![]() 在(0,1)内有两个实根。
在(0,1)内有两个实根。
(20)已知函数![]() 数列{
数列{![]() }(
}(![]() )的第一项
)的第一项![]() 以后各项
以后各项
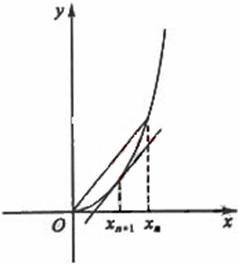
按如下方式取定:曲线![]() 处的切线与经过(0,0)和
处的切线与经过(0,0)和
(![]() 两点的直线平行(如图),求证:当n
两点的直线平行(如图),求证:当n![]() N+时,
N+时,
(Ⅰ)![]() ;
;
(Ⅱ)![]() 。
。
天津(理)
一、选择题(每小题5分)
(9)函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象
如图所示,则函数f(x)在开区间(a,b)内有极小值点()
(A)1个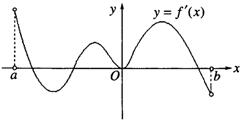
(B)2个
(C)3个
(D)4个
(10)已知函数y=f(x)的图象与函数y=ax(a>0且a=1)的图象关于直线y=x对称,
记g(x)=f(x)[f(x)+f(2)-1].若y=g(x)在区间[![]() ,2]上是增函数,
,2]上是增函数,
则实数a的取值范围是()
(A)[2,+∞)
(B)(0,1)∪(1,2)
(C)[![]() ,1)
(D)(0,
,1)
(D)(0,![]() ]
]
二、填空题(每小题4分)
(15)某公司一年购买某种货物400吨,每次都购买x吨,运费为4万元/次,
—年的总存储费用为4x万元,要使—年的总运费与总存储费用之和最小,
则x=___________吨.解答
(16)设函数f(x)=![]() ,点A0表示坐标原点,点An(n,f(n))(n∈N*).若向量
,点A0表示坐标原点,点An(n,f(n))(n∈N*).若向量
![]() θn是
θn是![]() 与
与![]() 的夹角(其中
的夹角(其中![]() =(1,0)),
=(1,0)),
设Sn=tanθl+tanθ2+…+tanθn,则![]() Sn=_____________.解答
Sn=_____________.解答
三、解答题
(20)(本小题满分12分)
已知函数f(x)=4x3-3x2cosθ+![]() cosθ,其中x∈R,θ为参数,且0≤θ<2π.
cosθ,其中x∈R,θ为参数,且0≤θ<2π.
(Ⅰ)当cosθ=0时,判断函数f(x)是否有极值;
(Ⅱ)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数θ,函数f(x)在区间
(2a-1,a)内都是增函数,求实数α的取值范围.
江苏
三、解答题
(20)(本小题满分16分,第一小问4分,第二小问满分6分,第三小问满分6分)
设a为实数,设函数![]() 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=![]() ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足![]() 的所有实数a
的所有实数a
辽宁(理)
一、选择提(每题5分)
(2)
设![]() 是R上的任意函数,则下列叙述正确的是(
)
是R上的任意函数,则下列叙述正确的是(
)
(A)![]() 是奇函数
(B)
是奇函数
(B)![]() 是奇函数
是奇函数
(C)
![]() 是偶函数
(D)
是偶函数
(D)
![]() 是偶函数
是偶函数
二、填空题(每题4分)
(13)
设 则
则 __________
__________
三、解答题
21.(本小题满分12分)
已知函数f(x)=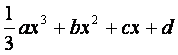 ,其中a
, b , c是以d为公差的等差数列,,
,其中a
, b , c是以d为公差的等差数列,,
且a>0,
d>0.设![]() [1-
[1-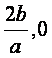 ]上,
]上,![]() 在
在![]() 处取得
处取得
最大值,在![]() ,将点
,将点![]() 依次记为A,
依次记为A,
B,
C.![]()
(I)求![]()
(II)若⊿ABC有一边平行于x轴,且面积为![]() ,求a
,d的值
,求a
,d的值
22.(本小题满分12分)
已知![]()
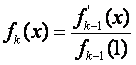 ,其中
,其中![]() ,设
,设![]() ,
,![]() .
.
(I)
写出![]() ;
;
(II)
证明:对任意的![]() ,恒有
,恒有![]() .
.
重庆(理)
一、选择题(每小题5分)
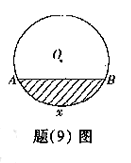
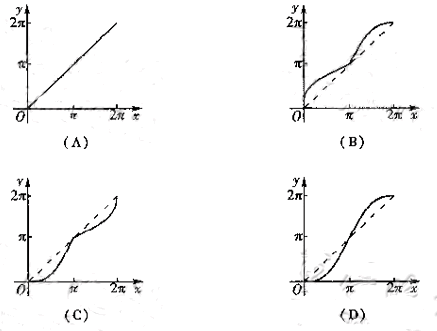
(9)如图所示,单位圆中弧![]() 的长为
的长为![]() ,
,![]() 表示
表示![]() 与弦
与弦![]() 所围成的
所围成的
弓形面积的2倍,则函数![]() 的图像是()
的图像是()
二、填空题(每小题4分)
(15)设![]() ,函数
,函数![]() 有最大值,则不等式
有最大值,则不等式
![]() 的解集为
。
解答
的解集为
。
解答
(16)已知变量![]() ,
,![]() 满足约束条件
满足约束条件![]() 。若目标
。若目标
函数![]() (其中
(其中![]() )仅在点
)仅在点![]() 处取得最大值,则
处取得最大值,则![]() 的取值范围
的取值范围
为 。解答
三、解答题
(20)(本小题满分13分)
已知函数![]() ,其中
,其中![]() 为常数。
为常数。
(Ⅰ)若![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若![]() ,且
,且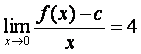 ,试证:
,试证:![]() ;
;
(21)(本小题满分12分)
已知定义域为![]() 的函数
的函数![]() 满足
满足![]() 。
。
(Ⅰ)若![]() ,求
,求![]() ;又若
;又若![]() ,求
,求![]() ;
;
(Ⅱ)设有且仅有一个实数![]() ,使得
,使得![]() ,求函数
,求函数![]() 的解析表达式;
的解析表达式;
湖南(理)
一、选择题(每题5分)
1.函数y=![]() 的定义域是(
)
的定义域是(
)
A.(3,+∞)
B.[3,![]() C.(4,+∞)
D.[4,+∞
C.(4,+∞)
D.[4,+∞![]()
4.“a=1”是“函数f(x)=|x-a|在区间[1,+∞)上为增函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
8.设函数f(x)=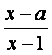 ,集合M={x|f(x)<0},P={x|f′(x)>0}.若M
,集合M={x|f(x)<0},P={x|f′(x)>0}.若M![]() P,则实数
P,则实数
a的取值范围是( )
A.(-∞,1)
B.(0,1)
C.(1,+∞)
D.[1,+∞![]()
三、解答题
19.(本小题满分14分)
已知函数f(x)=x-sinx,数列{an}满足:0<a1<1,an+1=f(an),n=1,2,3,….
证明:(Ⅰ)0<an+1<an<1;(Ⅱ)an+1<![]() an3.
an3.
湖北(理)
一、选择题(每题5分)
4.设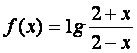 ,则
,则 的定义域为(
)
的定义域为(
)
A.(-4,0)![]() (0,4)
B.(-4,-1)
(0,4)
B.(-4,-1)![]() (1,4)
(1,4)
C.(-2,-1)![]() (1,2)
D.(-4,-2)
(1,2)
D.(-4,-2)![]() (2,4)
(2,4)
9.已知平面区域D由以A(1,3)、B(5,2)、C(3,1)为顶点的三角形内部
和边界组成。若在区域D上有无穷多个点(x,y)可使目标函数z=x+my取得最小值,
则m=( )
A.-2 B.-1 C.1 D.4
三、解答题
17.(本小题满分13分)
已知二次函数y=f(x)的图象经过坐标原点,其导函数为![]() .数列{
.数列{![]() }的
}的
前n项和为Sn,点![]() 均在函数y=f(x)的图象上。
均在函数y=f(x)的图象上。
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设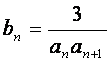 ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<![]() 对所有
对所有![]() 都成
都成
立的最小正整数m。
21.(本小题满分14分)
设x=3是函数f(x)=(x2+ax+b)e3-x(x∈R)的一个极值点。
(Ⅰ)求a与b的关系式(用a表示b),并求f(x)的单调区间;
(Ⅱ)设![]() >0,
>0,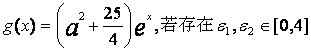 使得
使得![]() <1成立,
<1成立,
求a的取值范围。
广东
一、选择题(每题5分)
1.函数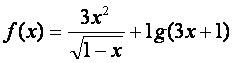 的定义域是()
的定义域是()
A.(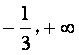 ) B.(
) B.(![]() ) C.(
) C.(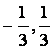 ) D.(
) D.(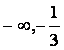 )
)
3.下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.函数![]() 的反函数y=f-1(x)的图像与y轴交于点P(0,2)(如图),
的反函数y=f-1(x)的图像与y轴交于点P(0,2)(如图),
则方程f(x)=0在![]() 上的根是x=()
上的根是x=()
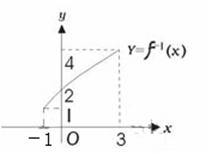
A.4 B.3 C.2 D.1
三、解答题
18.(本小题满分14分)
设函数f(x)=-x3+3x+2分别在x1、x2处取得极小值、极大值。xoy平面
上点A、B的坐标分别为(x1,f(x1))、(x2,f(x2))。该平面上动点P满
足![]() ,点Q是点P关于直线y=2(x-4)的对称点,求:
,点Q是点P关于直线y=2(x-4)的对称点,求:
(Ⅰ)点A、B的坐标:
(Ⅱ)动点Q的轨迹方程。
20.(本小题满分12分)
A是由定义在[2,4]上且满足如下条件的函数![]() (x)组成的集合:
(x)组成的集合:
①对任意的![]() 都有
都有![]() (2x)
(2x)![]() ;②存在常数L(0<L<1),
;②存在常数L(0<L<1),
使得对任意的x1,x2![]() [1,2],都有|
[1,2],都有|![]() (2x1)-
(2x1)-![]() (2x2)|
(2x2)|![]() .
.
(Ⅰ)设![]() (x)=
(x)=![]() 证明:
证明:![]() (x)
(x)![]() A:
A:
(Ⅱ)设![]() (x)
(x)![]() ,如果存在x0
,如果存在x0![]() (1,2),使得x0=
(1,2),使得x0=![]() (2x0),
(2x0),
那么这样的x0是唯一的:
(Ⅲ)设![]()
![]() 任取x1
任取x1![]() (1,2),令xn+1=
(1,2),令xn+1=![]() (2xn),n=1,2……证明:给定
(2xn),n=1,2……证明:给定
正整数k,对任意的正整数p,成立不等式 。
。
北京(理)
一、选择题(每题5分)
(5)已知f(x)= 是(-∞,+∞)上的减函数,那么a的
是(-∞,+∞)上的减函数,那么a的
取值范围是( )
(A)(0,1)
(B)(0,![]() )
)
(C)[![]() )
(C)[
)
(C)[![]() ,1)
,1)
(6)在下列四个函数中,满足性质:“对于区间(1,2)上的任意x1,x2
(x1≠x2),|f(x2)-f(x1)|<|x2-x1|恒成立”的只有( )
(A)f(x)=![]() (B)f(x)=|x|
(B)f(x)=|x|
(C)f(x)=2x (D)f(x)=x2
三、解答题
(16)(本小题共13分)
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)
的图象经过点(1,0),(2,0),如图所示,求:

(Ⅰ)x0的值;
(Ⅱ)a,b,c的值.
上海(理)
一、填空题(每小题4分)
3.若函数![]() =
=![]() (
(![]() >0,且
>0,且![]() ≠1)的反函数的图像过点(2,-1),
≠1)的反函数的图像过点(2,-1),
则![]() =
.解答
=
.解答
三、解答题
22.(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分6分,
第3小题满分9分)
已知函数![]() =
=![]() +
+![]() 有如下性质:如果常数
有如下性质:如果常数![]() >0,那么该函数在
>0,那么该函数在
![]() 0,
0,![]()
![]() 上是减函数,在
上是减函数,在![]()
![]() ,+∞
,+∞![]() 上是增函数.
上是增函数.
(1)如果函数![]() =
=![]() +
+![]() (
(![]() >0)的值域为
>0)的值域为![]() 6,+∞
6,+∞![]() ,求
,求![]() 的值;
的值;
(2)研究函数![]() =
=![]() +
+![]() (常数
(常数![]() >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(3)对函数![]() =
=![]() +
+![]() 和
和![]() =
=![]() +
+![]() (常数
(常数![]() >0)作出推广,使它们都是
>0)作出推广,使它们都是
你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必
证明),并求函数![]() =
= +
+ (
(![]() 是正整数)在区间[
是正整数)在区间[![]() ,2]上
,2]上
的最大值和最小值(可利用你的研究结论).
山东(理)
一、选择题(每小题5分)
2.函数y=1+ax(0<a<1)的反函数的图象大致是( )

6.已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),则f(6)的值为()
(A)-1 (B)0 (C)1 (D)2
8.设p∶x2-x-20>0,q∶ <0,则p是q的()
<0,则p是q的()
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
三、解答题
18.(本小题满分12分)
设函数f(x)=ax-(a+1)ln(x+1),其中a≥-1.求f(x)的单调区间.
江西(理)
一、选择题(每题5分)
12.某地一年内的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图(1)所示,
已知该年的平均气温
为10℃.令C(t)表示时间段[0,t]的平均气温,C(t)与t之间的函数关系用下
列图象表示,则正确的
应该是( )


二、填空题(每题4分)
14.设f(t)=log3(x+6)的反函数为f-1(x),若[f-1(m)+6]· [f-1(n)+6]=27,
则f(m+n)=_______.
三、解答题
17.(本小题满分12分)
已知函数f(x)=x3+ax2+bx+c在x=-![]() 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
陕西(理)
一、选择题(每小题5分)
4.设函数![]() 的图像过点
的图像过点![]() ,其反函数的图像
,其反函数的图像
过点![]() ,则
,则![]() 等于()
等于()
(A)3 (B)4 (C)5 (D)6
10.已知函数![]() 若
若![]() 则()
则()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]() 与
与![]() 的大小不能确定
的大小不能确定
12.为确保信息安全,信息需加密传输,发送方由明文![]() 密文(加密),
密文(加密),
接收方由密文![]() 明文(解密),已知加密规则为:明文
明文(解密),已知加密规则为:明文![]() 对应密文
对应密文
![]() 例如,明文
例如,明文![]() 对应密文
对应密文![]() 当接收方收到
当接收方收到
密文![]() 时,则解密得到的明文为()
时,则解密得到的明文为()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
三、解答题
(22)(本小题满分14分)
已知函数 且存在
且存在 使
使![]()
(I)证明:![]() 是R上的单调增函数;
是R上的单调增函数;
(II)设
其中 ![]()
证明:![]()
(III)证明:
安徽(理)
一、选择题(每题5分)
(5)函数y= 的反函数是(
)
的反函数是(
)
(A)y= (B)y=
(B)y=
(C)y=
![]() (D)y=
(D)y=
(6)将函数y=sin![]() 的图像按向量
的图像按向量![]() 平移,平移后的图像如图所示,
平移,平移后的图像如图所示,
则平移后的图像所对应的函数解析式是( )

(A)y=sin( )
)
(B)y=sin( )
)
(C)y=sin( )
)
(D)y=sin(![]() )
)
二、填空题(每题4分)
(15)函数f(x)对于任意实数x满足条件f(x+2)=![]() ,若f(1)=-5,
,若f(1)=-5,
则f(f(5))= ___________。
三、解答题
(20)(本小题满分12分)
已知函数f(x)在R上有定义,对任意实数a>0和任意实数x,都有
![]()
(Ⅰ)证明f(0)=0:
(Ⅱ)证明 ,其中k和h均为常数:
,其中k和h均为常数:
(Ⅲ)当(Ⅱ)中的k>0,设g(x)= 讨论g(x)在(0,+
讨论g(x)在(0,+![]() )内
)内
的单调性并求极值。
四川(理)
一、选择题(每小题5分)
(3)已知 ,下面结论正确的是()
,下面结论正确的是()
(A)![]() 在
在![]() 处连续
(B)
处连续
(B)![]()
(C)![]() (D)
(D)![]()
三、解答题
(22)(本小题满分14分)
已知函数 ,
,![]() 的导函数是
的导函数是![]() ,
,
对任意两个不相等的正数![]() ,证明:
,证明:
(Ⅰ)当![]() 时,
时,
(Ⅱ)当![]() 时,
时,![]()
全国卷(Ⅰ)理
一、选择题(每题5分)
(2)已知函数![]() 的图像与函数
的图像与函数![]() 的图像关于直线
的图像关于直线![]() 对称,则(
)
对称,则(
)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
三、解答题
(21)(本小题满分14分)
已知函数 .
.
(Ⅰ)设![]() 讨论
讨论![]() 的单调性;
的单调性;
(Ⅱ)若对任意![]() 恒有
恒有![]() ,求a的取值范围。
,求a的取值范围。
全国卷(Ⅱ)理
一、选择题(每小题5分)
(6)函数![]() 的反函数为
的反函数为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(8)函数![]() 的图像与函数
的图像与函数![]() 的图像关于原点对称,
的图像关于原点对称,
则![]() 的表达式为
的表达式为
(A) (B)
(B)
(C)![]() (D)
(D)![]()
(12)函数 的最小值为()
的最小值为()
(A)190 (B)171 (C)90 (D)45
三、解答题
(20)(本小题满分12分)
设函数![]() 若对所有的
若对所有的![]() 都有
都有![]() 成立,
成立,
求实数![]() 的取值范围。
的取值范围。