三、解答题
(20)(本小题满分12分)
已知函数f(x)在R上有定义,对任意实数a>0和任意实数x,都有
![]()
(Ⅰ)证明f(0)=0:
(Ⅱ)证明 ,其中k和h均为常数:
,其中k和h均为常数:
(Ⅲ)当(Ⅱ)中的k>0,设g(x)=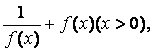 讨论g(x)在(0,+
讨论g(x)在(0,+![]() )内
)内
的单调性并求极值。
本小题主要考查函数的概念、导数应用、函数的单调区间和极值等知识,考
查运用数学知识解决问题及推理的能力.满分12分.
(Ⅰ)证明:对于任意的![]() 均有
均有
![]() ①
①
在①中取![]() 即得
即得![]()
![]()
![]() ②
②
(Ⅱ)证明:当![]() 时,由①得
时,由①得
![]()
取![]() ,则有
,则有
![]() ;
③
;
③
当![]() 时,由①得
时,由①得
![]()
取![]() 则有
则有
![]() ④
④
综合②、③、④得

(Ⅲ)解法1:由(Ⅱ)中的③知,当![]() 时,
时,
从而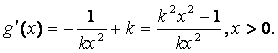
又因为![]() 由此可得
由此可得
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值2 |
|
所以![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,
内单调递增,
在 处取得极小值2.
处取得极小值2.
解法2:由(Ⅱ)中的③知,当![]() 时,
时,![]()
设![]() 且
且![]() ,则
,则

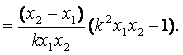
又因为![]() 所以
所以
![]() 当
当![]() 时,
时,![]() ;
;
![]() 当
当 时,
时,![]()
所以![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,在
内单调递增,在 处取得极小值2.
处取得极小值2.