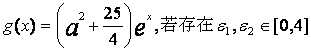 使得
使得三、解答题
21.(本小题满分14分)
设x=3是函数f(x)=(x2+ax+b)e3-x(x∈R)的一个极值点。
(Ⅰ)求a与b的关系式(用a表示b),并求f(x)的单调区间;
(Ⅱ)设![]() >0,
>0,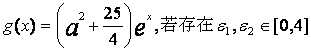 使得
使得![]() <1成立,
<1成立,
求a的取值范围。
点评:本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学
知识解决问题的能力。
解:(Ⅰ)f `(x)=-[x2+(a-2)x+b-a ]e3-x,
由f `(3)=0,得 -[32+(a-2)3+b-a ]e3-3=0,即得b=-3-2a,
则 f `(x)=[x2+(a-2)x-3-2a-a ]e3-x
=-[x2+(a-2)x-3-3a ]e3-x=-(x-3)(x+a+1)e3-x.
令f `(x)=0,得x1=3或x2=-a-1,由于x=3是极值点,
所以x+a+1≠0,那么a≠-4.
当a<-4时,x2>3=x1,则
在区间(-∞,3)上,f `(x)<0, f (x)为减函数;
在区间(3,―a―1)上,f `(x)>0,f (x)为增函数;
在区间(―a―1,+∞)上,f `(x)<0,f (x)为减函数。
当a>-4时,x2<3=x1,则
在区间(-∞,―a―1)上,f `(x)<0, f (x)为减函数;
在区间(―a―1,3)上,f `(x)>0,f (x)为增函数;
在区间(3,+∞)上,f `(x)<0,f (x)为减函数。
(Ⅱ)由(Ⅰ)知,当a>0时,f (x)在区间(0,3)上的单调递增,在区间
(3,4)上单调递减,那么f (x)在区间[0,4]上的值域是[min(f (0),f (4) ),f (3)],
而f (0)=-(2a+3)e3<0,f (4)=(2a+13)e-1>0,f (3)=a+6,
那么f (x)在区间[0,4]上的值域是[-(2a+3)e3,a+6].
又![]() 在区间[0,4]上是增函数,
在区间[0,4]上是增函数,
且它在区间[0,4]上的值域是[a2+![]() ,(a2+
,(a2+![]() )e4],
)e4],
由于(a2+![]() )-(a+6)=a2-a+
)-(a+6)=a2-a+![]() =(
=(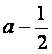 )2≥0,所以只须仅须
)2≥0,所以只须仅须
(a2+![]() )-(a+6)<1且a>0,解得0<a<
)-(a+6)<1且a>0,解得0<a<![]() .
.
故a的取值范围是(0,![]() )。
)。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。