^{三、解答题}

（16）（本小题共13分）

 已知函数f（x）=ax³+bx²+cx在点x₀处取得极大值5，其导函数y=f′（x）

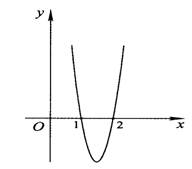
的图象经过点（1，0），（2，0），如图所示，求：

（Ⅰ）x₀的值；

（Ⅱ）a，b，c的值.

    解法一：

（Ⅰ）由图象可知，在（-∞，1）上f′（x）＞0，在（1，2）上f′（x）

＜0，在（2，+∞）上f′（x）＞0，

故f（x）在（-∞，1），（2，+∞）上递增，在（1，2）上递减，

因此f（x）在x=1处取得极大值，所以x₀=1.

（Ⅱ）f′（x）=3ax²+2bx+c，

   由f′（1）=0，f′（2）=0，f（1）=5，

   得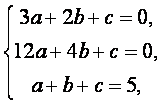

   解得a=2，b= -9，c=12.

   解法二：

（Ⅰ）同解法一.

（Ⅱ）设f′（x）=m（x-1）(x-2)=mx²-3mx+2m,

      又f′（x）=3ax²+2bx+c,

      所以a=

      f(x)=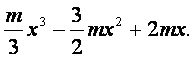

      由f（1）=5，

      即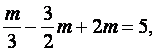

      得m=6，

      所以a=2，b= -9，c=12.