三、解答题

22．（本题满分18分）本题共有3个小题，第1小题满分3分，第2小题满分6分，

第3小题满分9分）

已知函数＝＋有如下性质：如果常数＞0，那么该函数在

0，上是减函数，在，＋∞上是增函数．

（1）如果函数＝＋（＞0）的值域为6，＋∞，求的值；

（2）研究函数＝＋（常数＞0）在定义域内的单调性，并说明理由；

（3）对函数＝＋和＝＋（常数＞0）作出推广，使它们都是

你所推广的函数的特例．研究推广后的函数的单调性（只须写出结论，不必

证明），并求函数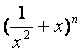＝＋（是正整数）在区间[，2]上

的最大值和最小值（可利用你的研究结论）．

解：（1）易知，时，。

（2）＝＋是偶函数。易知，该函数在上是减函数，

在上是增函数；  则该函数在上是减函数，

在上是增函数。

（3）推广：函数，当为奇数时，，

是减函数；，是增函数。                                             

   ，是增函数；，是减函数。当为偶数时，

，是减函数；，是增函数。   ，

是减函数；，是增函数。＝＋

当时，。

        ∴，是减函数；，是增函数。

        ∵ 

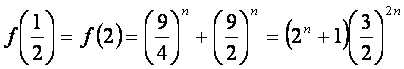
∴函数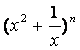＝＋在区间[，2]上的最大值

为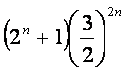，最小值为。