福建（理）

选择题（每小题5分）

2．已知等差数列中，，则的值是 

       A．15      B．30       C．31      D．64

解答

填空题（每小题4分）

13．展开式中的常数项是           （用数字作答）

解答

解答题

22．（本小题满分14分）

已知数列{an}满足a1=a, an+1=1+我们知道当a取不同的值时，得到不同

的数列，如当a=1时，得到无穷数列：

（Ⅰ）求当a为何值时a4=0；

（Ⅱ）设数列{bn­}满足b1=－1, bn+1=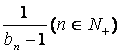，求证a取数列{bn}中的

任一个数，都可以得到一个有穷数列{an}；

（Ⅲ）若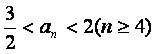，求a的取值范围.

解答

浙江（理）

选择题(每小题5分)

5．在(1－x)⁵＋(1－x)⁶＋(1－x)⁷＋(1－x)⁸的展开式中，含x³的项的系数是(    )

(A) 74   (B) 121    (C) －74    (D) －121

解答

解答题

20．设点(，0)，和抛物线：y＝x2＋an x＋bn(n∈N*)，其中

a_n＝－2－4_n－，由以下方法得到：

   x₁＝1，点P₂(x₂，2)在抛物线C₁：y＝x₂＋a₁x＋b₁上，点A₁(x₁，0)到P₂的距离是

   A₁到C₁上点的最短距离，…，点在抛物线：y＝x₂＋a_n x＋b_n上，

   点(，0)到的距离是 到 上点的最短距离．

   (Ⅰ)求x₂及C₁的方程．

   (Ⅱ)证明{}是等差数列．

解答

天津（理）

填空题(每小题4分)

（13）在数列{a_n}中,a₁=1,a₂=2,且则=_____．

解答

解答题

  （18）（本小题满分12分）

已知

 （Ⅰ）当时，求数列的前n项和

 （Ⅱ）求

  解答

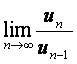
江苏

选择题(每小题5分)

3.在各项都为正数的等比数列中，首项，前三项和为21，

则=（  ）

A．33        B．72       C．84       D．189

解答

 9.设，则的展开式中的系数不可能是（  ）

 A．10         B．40       C．50        D．80

解答

填空题(每小题4分)

 16.若，,则=__________

解答

解答题

23.（本小题满分14分，第一小问满分2分，第二.第三小问满分各6分）

设数列的前项和为，已知，且

    ，其中A.B为常数

  ⑴求A与B的值；

  ⑵证明：数列为等差数列；

  ⑶证明：不等式对任何正整数都成立

解答

辽宁

填空题(每小题4分)

13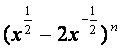．的展开式中常数项是             .

解答

解答题

19．（本小题满分12分）

  已知函数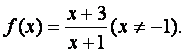设数列}满足，数列}满足

    （Ⅰ）用数学归纳法证明；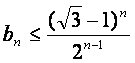

    （Ⅱ）证明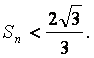

解答

重庆（理）

选择题(每小题5分)

8．若ⁿ展开式中含项的系数与含项的系数之比为－5，则n等于

    A．4        B．6        C．8         D．10

解答

解答题

22．（本小题满分12分）

       数列{an}满足.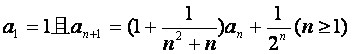

    （Ⅰ）用数学归纳法证明：；

  （Ⅱ）已知不等式，其中无理数

e=2.71828….

解答

湖南（理）

选择题(每小题5分)

3．已知数列{log₂(a_n－1)}（n∈N^*）为等差数列，且a₁＝3，a₂＝5，则

　　= （　  ）

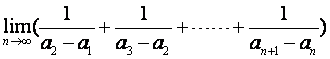　　A．2　　  B．　　    C．1　　     D．

解答

填空题(每小题4分)

11．一工厂生产了某种产品16800件，它们来自甲．乙．丙3条生产线，

为检查这批产品的质量，决定采用分层抽样的方法进行抽样，已知甲．

乙．丙三条生产线抽取的个体数组成一个等差数列，则乙生产线生产

了　　　   件产品.

解答

12．在的展开式中，x 2项的系数是　　　　.

（用数字作答）解答

解答题

20．（本小题满分14分）

自然状态下的鱼类是一种可再生资源，为持续利用这一资源，需从宏观上考察

其再生能力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量，

n∈N*，且x1＞0.不考虑其它因素，设在第n年内鱼群的繁殖量及捕捞量都与xn成

正比，死亡量与xn2成正比，这些比例系数依次为正常数a，b，c.

   （Ⅰ）求xn+1与xn的关系式；

   （Ⅱ）猜测：当且仅当x1，a，b，c满足什么条件时，每年年初鱼群的总量

保持不变？（不要求证明）

　 （Ⅱ）设a＝2，b＝1，为保证对任意x1∈（0,2），都有xn＞0，n∈N*，

则捕捞强度b的最大允许值是多少？证明你的结论.

解答

湖北（理）

填空题(每小题4分)

14．的展开式中整理后的常数项等于             

解答

15．设等比数列{}的公比为q，前n项和为，若，，成等差数列，

则q的值为            

解答

广东

选择题(每小题5分)

10．已知数列（    ）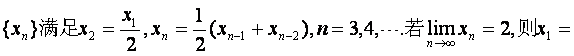

       A．       B．3       C．4         D．5

解答

填空题(每小题4分)

13．已知的展开式中的系数与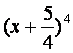的展开式中x₃的系数相等，

则=        .

解答

北京（理）

填空题(每小题5分)

(11)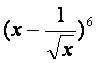的展开式中的常数项是           (用数字作答)

解答

(14) 已知n次多项式=

    如果在一种算法中，计算(k=2，3，4，…，n)的值需要k-1次乘法，

    计算的值共需要9次运算(6次乘法，3次加法)，那么计算的值

    共需要      次运算．

    下面给出一种减少运算次数的算法： =Pn+1()=Pn()+ 

    (k=0,l，2，…，n-1)．利用该算法，计算的值共需要6次运算，

    计算的值共需要              次运算

解答

解答题

(19)(本小题共12分)

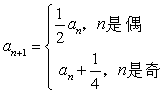设数列的首项,且,记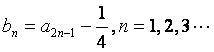

(Ⅰ)求

(Ⅱ)判断数列是否为等比数列,并证明你的结论;

(Ⅲ)求

解答

上海（理）

填空题(每小题4分)

4.在的展开式中，的系数是15，则实数______________

解答

12.用n个不同的实数可得到个不同的排列，每个排列为一行写成一个

行的数阵对第行，记 

例如：用1，2，3可得数阵如下，

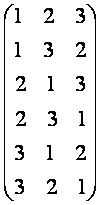
由于此数阵中每一列各数之和都

是12，所以，

那么，在用1，2，3，4，5形成的数阵中，

___________________

     解答

山东（理）

选择题(每小题5分)

（5）如果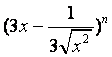的展开式中各项系数之和为128，则展开式中的系数是

   （A）           (B)           (C)           (D) 

解答

解答题

 (21) （本小题满分12分）已知数列的首项前项和为，

且

（I）证明数列是等比数列；

（II）令，求函数在点处的导数

并比较与的大小

解答

江西（理）

选择题(每小题5分)

4．的展开式中，含x的正整数次幂的项共有

       A．4项      B．3项       C．2项     D．1项

解答

解答题

21．（本小题满分12分）

已知数列

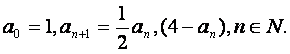
 （1）证明

 （2）求数列的通项公式an.

解答

全国卷（Ⅰ）理

填空题(每小题4分)

（14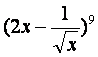）的展开式中，常数项为           （用数字作答）

解答

解答题

（19）（本大题满分12分）

设等比数列的公比为，前n项和

（Ⅰ）求的取值范围；

（Ⅱ）设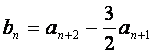，记的前n项和为，试比较与的大小

解答

全国卷（Ⅱ）理

选择题(每小题5分)

（11）如果，，…，为各项都大于零的等差数列，公差，则

（A）（B）（C）++（D）=

解答

解答题

（18） （本小题满分12分）

已知是各项均为正数的等差数列，、、成等差数列．又，…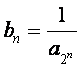

（Ⅰ）证明为等比数列；

（Ⅱ）如果无穷等比数列各项的和，求数列的首项和公差．

（注：无穷数列各项的和即当时数列前项和的极限）

解答

全国卷（Ⅲ）理

选择题(每小题5分)

3.在(x-1)(x+1)⁸的展开式中x⁵的系数是(  )

A.-14           B.14           C.-28        D.28

解答

解答题

20.（本小题满分12分）

    在等差数列{an}中，公差d≠0,且a2是a1和a4的等比中项,已知a1,a3,

成等比数列，求数列k1,k2,k3,…,kn的通项kn 

解答